Advertisements
Advertisements
प्रश्न
Find the value of x, if tan `[sec^(-1) (1/x) ] = sin ( tan^(-1) 2) , x > 0 `.
उत्तर
Let sec-1 `(1/x) = theta`
` ⇒ sec theta = 1/x`
⇒ cos θ = x
⇒ tan ` (sec^(-1) (1/x)) = tan theta = sqrt(1 -x^2 ) /x ` ...(1)
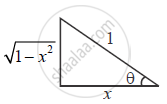
Now consider,
sin ( tan -1 2 )
Let tan-1 2 = Φ
tan Φ = 2
sin ( tan-1 2) = sin Φ = `2/sqrt(5) ` ...(ii)
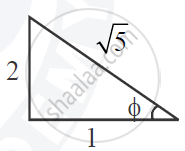
From (i) and (ii)
`sqrt(1- x^2 )/x = 2/sqrt(5)`
5(1 - x2 ) = 4x2
`x = +- sqrt(5)/3 " but " x > 0 ⇒ x = sqrt(5)/3`
APPEARS IN
संबंधित प्रश्न
Solve the equation for x:sin−1x+sin−1(1−x)=cos−1x
If `cos^-1( x/a) +cos^-1 (y/b)=alpha` , prove that `x^2/a^2-2(xy)/(ab) cos alpha +y^2/b^2=sin^2alpha`
Solve the following for x :
`tan^(-1)((x-2)/(x-3))+tan^(-1)((x+2)/(x+3))=pi/4,|x|<1`
Evaluate the following:
`cos^-1(cos4)`
Evaluate the following:
`sec^-1(sec pi/3)`
Evaluate the following:
`cosec^-1(cosec (6pi)/5)`
Evaluate the following:
`cosec^-1(cosec (11pi)/6)`
Evaluate the following:
`cot^-1(cot (19pi)/6)`
Evaluate the following:
`cot^-1{cot (-(8pi)/3)}`
Write the following in the simplest form:
`tan^-1{sqrt(1+x^2)-x},x in R `
Write the following in the simplest form:
`tan^-1{(sqrt(1+x^2)-1)/x},x !=0`
Evaluate:
`tan{cos^-1(-7/25)}`
`tan^-1x+2cot^-1x=(2x)/3`
Prove the following result:
`sin^-1 12/13+cos^-1 4/5+tan^-1 63/16=pi`
Sum the following series:
`tan^-1 1/3+tan^-1 2/9+tan^-1 4/33+...+tan^-1 (2^(n-1))/(1+2^(2n-1))`
`2tan^-1 3/4-tan^-1 17/31=pi/4`
Solve the following equation for x:
`tan^-1 1/4+2tan^-1 1/5+tan^-1 1/6+tan^-1 1/x=pi/4`
If `sin^-1x+sin^-1y+sin^-1z=(3pi)/2,` then write the value of x + y + z.
If 4 sin−1 x + cos−1 x = π, then what is the value of x?
Wnte the value of the expression \[\tan\left( \frac{\sin^{- 1} x + \cos^{- 1} x}{2} \right), \text { when } x = \frac{\sqrt{3}}{2}\]
If \[\cos\left( \sin^{- 1} \frac{2}{5} + \cos^{- 1} x \right) = 0\], find the value of x.
Find the value of \[\tan^{- 1} \left( \tan\frac{9\pi}{8} \right)\]
If x < 0, y < 0 such that xy = 1, then tan−1 x + tan−1 y equals
\[\text{ If }\cos^{- 1} \frac{x}{3} + \cos^{- 1} \frac{y}{2} = \frac{\theta}{2}, \text{ then }4 x^2 - 12xy \cos\frac{\theta}{2} + 9 y^2 =\]
If 4 cos−1 x + sin−1 x = π, then the value of x is
In a ∆ ABC, if C is a right angle, then
\[\tan^{- 1} \left( \frac{a}{b + c} \right) + \tan^{- 1} \left( \frac{b}{c + a} \right) =\]
\[\cot\left( \frac{\pi}{4} - 2 \cot^{- 1} 3 \right) =\]
Write the value of \[\cos^{- 1} \left( - \frac{1}{2} \right) + 2 \sin^{- 1} \left( \frac{1}{2} \right)\] .
