Advertisements
Advertisements
प्रश्न
Find the value of x, if tan `[sec^(-1) (1/x) ] = sin ( tan^(-1) 2) , x > 0 `.
उत्तर
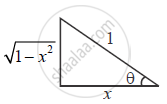
Let sec-1 `(1/x) = theta`
` ⇒ sec theta = 1/x`
⇒ cos θ = x
⇒ tan ` (sec^(-1) (1/x)) = tan theta = sqrt(1 -x^2 ) /x ` ...(1)
Now consider,
sin ( tan -1 2 )
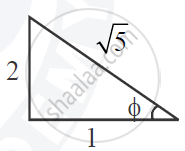
Let tan-1 2 = Φ
tan Φ = 2
sin ( tan-1 2) = sin Φ = `2/sqrt(5) ` ...(ii)
From (i) and (ii)
`sqrt(1- x^2 )/x = 2/sqrt(5)`
5(1 - x2 ) = 4x2
`x = +- sqrt(5)/3 " but " x > 0 ⇒ x = sqrt(5)/3`
APPEARS IN
संबंधित प्रश्न
Prove that :
`2 tan^-1 (sqrt((a-b)/(a+b))tan(x/2))=cos^-1 ((a cos x+b)/(a+b cosx))`
If sin [cot−1 (x+1)] = cos(tan−1x), then find x.
Find the domain of definition of `f(x)=cos^-1(x^2-4)`
`sin^-1(sin (7pi)/6)`
`sin^-1(sin (17pi)/8)`
`sin^-1(sin4)`
`sin^-1(sin12)`
Evaluate the following:
`sec^-1(sec pi/3)`
Evaluate the following:
`sec^-1(sec (25pi)/6)`
Evaluate:
`sec{cot^-1(-5/12)}`
Evaluate: `sin{cos^-1(-3/5)+cot^-1(-5/12)}`
Evaluate:
`sin(tan^-1x+tan^-1 1/x)` for x < 0
`4sin^-1x=pi-cos^-1x`
Find the value of `tan^-1 (x/y)-tan^-1((x-y)/(x+y))`
`2tan^-1 3/4-tan^-1 17/31=pi/4`
Solve the following equation for x:
`tan^-1((2x)/(1-x^2))+cot^-1((1-x^2)/(2x))=(2pi)/3,x>0`
Solve the following equation for x:
`cos^-1((x^2-1)/(x^2+1))+1/2tan^-1((2x)/(1-x^2))=(2x)/3`
Write the value of cos−1 (cos 350°) − sin−1 (sin 350°)
Write the value of \[\tan^{- 1} \frac{a}{b} - \tan^{- 1} \left( \frac{a - b}{a + b} \right)\]
If \[\tan^{- 1} (\sqrt{3}) + \cot^{- 1} x = \frac{\pi}{2},\] find x.
Write the value of \[\cos^{- 1} \left( \cos\frac{14\pi}{3} \right)\]
If \[\tan^{- 1} \left( \frac{\sqrt{1 + x^2} - \sqrt{1 - x^2}}{\sqrt{1 + x^2} + \sqrt{1 - x^2}} \right)\] = α, then x2 =
The number of real solutions of the equation \[\sqrt{1 + \cos 2x} = \sqrt{2} \sin^{- 1} (\sin x), - \pi \leq x \leq \pi\]
\[\text{ If }\cos^{- 1} \frac{x}{3} + \cos^{- 1} \frac{y}{2} = \frac{\theta}{2}, \text{ then }4 x^2 - 12xy \cos\frac{\theta}{2} + 9 y^2 =\]
Let f (x) = `e^(cos^-1){sin(x+pi/3}.`
Then, f (8π/9) =
If tan−1 (cot θ) = 2 θ, then θ =
If x = a (2θ – sin 2θ) and y = a (1 – cos 2θ), find \[\frac{dy}{dx}\] When \[\theta = \frac{\pi}{3}\] .
If \[\tan^{- 1} \left( \frac{1}{1 + 1 . 2} \right) + \tan^{- 1} \left( \frac{1}{1 + 2 . 3} \right) + . . . + \tan^{- 1} \left( \frac{1}{1 + n . \left( n + 1 \right)} \right) = \tan^{- 1} \theta\] , then find the value of θ.
The value of tan `("cos"^-1 4/5 + "tan"^-1 2/3) =`
The equation sin-1 x – cos-1 x = cos-1 `(sqrt3/2)` has ____________.
