Advertisements
Advertisements
प्रश्न
Prove that:
उत्तर
L.H.S. =
=
=
=
=
=
=
=
=
=
= R.H.S.
APPEARS IN
संबंधित प्रश्न
Find the value of x in the following :
tan 3x = sin 45º cos 45º + sin 30º
If θ is an acute angle and sin θ = cos θ, find the value of 2 tan2 θ + sin2 θ – 1
If tan (A + B) =
Evaluate the following:
Evaluate the following :
Evaluate the following :
sin 35° sin 55° − cos 35° cos 55°
Express each one of the following in terms of trigonometric ratios of angles lying between 0° and 45°
cosec 54° + sin 72°
Prove that tan 20° tan 35° tan 45° tan 55° tan 70° = 1
Prove the following
Without using trigonometric tables, prove that:
cos54° cos36° − sin54° sin36° = 0
Express each of the following in terms of trigonometric ratios of angles lying between 0° and 45°.
sec78° + cosec56°
If sin x = cos y, then x + y = 45° ; write true of false
find the value of: tan 30° tan 60°
prove that:
tan (2 x 30°) =
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratio: cos 45°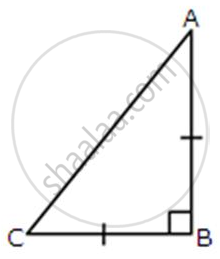
If sec A = cosec A and 0° ∠A ∠90°, state the value of A
For any angle θ, state the value of: sin2 θ + cos2 θ
If A = 30°;
show that:
4 cos A cos (60° - A). cos (60° + A) = cos 3A
Without using tables, evaluate the following: sin230° sin245° + sin260° sin290°.
Without using tables, evaluate the following: (sin90° + sin45° + sin30°)(sin90° - cos45° + cos60°).
Prove that : cos60° . cos30° - sin60° . sin30° = 0
Prove that : sec245° - tan245° = 1
Find the value of x in the following: 2 sin3x =
If sinθ = cosθ and 0° < θ<90°, find the value of 'θ'.
Without using table, find the value of the following:
If A = 30° and B = 60°, verify that: sin (A + B) = sin A cos B + cos A sin B
If A = 30° and B = 60°, verify that: cos (A + B) = cos A cos B - sin A sin B
If sin(A - B) =
Find the value of the following:
