Advertisements
Advertisements
प्रश्न
Solve the equation 27x2 – 10x + 1 = 0
उत्तर
The given quadratic equation is 27x2 – 10x + 1 = 0
On comparing the given equation with ax2 + bx + c = 0, we obtain
a = 27, b = –10, and c = 1
Therefore, the discriminant of the given equation is
D = b2 – 4ac = (–10)2 – 4 × 27 × 1 = 100 – 108 = –8
Therefore, the required solutions are
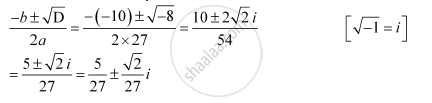
APPEARS IN
संबंधित प्रश्न
Solve the equation –x2 + x – 2 = 0
Solve the equation x2 + 3x + 5 = 0
Solve the equation x2 – x + 2 = 0
Solve the equation `sqrt3 x^2 - sqrt2x + 3sqrt3 = 0`
Solve the equation `x^2 + x + 1/sqrt2 = 0`
For any two complex numbers z1 and z2, prove that Re (z1z2) = Re z1 Re z2 – Imz1 Imz2
Solve the equation 21x2 – 28x + 10 = 0
\[x^2 + 2x + 5 = 0\]
\[21 x^2 + 9x + 1 = 0\]
\[27 x^2 - 10 + 1 = 0\]
\[2 x^2 + x + 1 = 0\]
\[\sqrt{2} x^2 + x + \sqrt{2} = 0\]
Solving the following quadratic equation by factorization method:
\[x^2 + 10ix - 21 = 0\]
Solve the following quadratic equation:
\[x^2 - \left( 5 - i \right) x + \left( 18 + i \right) = 0\]
Solve the following quadratic equation:
\[\left( 2 + i \right) x^2 - \left( 5 - i \right) x + 2 \left( 1 - i \right) = 0\]
Solve the following quadratic equation:
\[x^2 - \left( 2 + i \right) x - \left( 1 - 7i \right) = 0\]
Solve the following quadratic equation:
\[i x^2 - 4 x - 4i = 0\]
Solve the following quadratic equation:
\[2 x^2 + \sqrt{15}ix - i = 0\]
Solve the following quadratic equation:
\[2 x^2 - \left( 3 + 7i \right) x + \left( 9i - 3 \right) = 0\]
If roots α, β of the equation \[x^2 - px + 16 = 0\] satisfy the relation α2 + β2 = 9, then write the value P.
Write the number of quadratic equations, with real roots, which do not change by squaring their roots.
If α, β are roots of the equation \[x^2 + lx + m = 0\] , write an equation whose roots are \[- \frac{1}{\alpha}\text { and } - \frac{1}{\beta}\].
If α, β are roots of the equation \[x^2 - a(x + 1) - c = 0\] then write the value of (1 + α) (1 + β).
If a, b are the roots of the equation \[x^2 + x + 1 = 0, \text { then } a^2 + b^2 =\]
The number of real roots of the equation \[( x^2 + 2x )^2 - (x + 1 )^2 - 55 = 0\] is
If α, β are the roots of the equation \[x^2 + px + 1 = 0; \gamma, \delta\] the roots of the equation \[x^2 + qx + 1 = 0, \text { then } (\alpha - \gamma)(\alpha + \delta)(\beta - \gamma)(\beta + \delta) =\]
The number of real solutions of \[\left| 2x - x^2 - 3 \right| = 1\] is
If the roots of \[x^2 - bx + c = 0\] are two consecutive integers, then b2 − 4 c is
The value of a such that \[x^2 - 11x + a = 0 \text { and } x^2 - 14x + 2a = 0\] may have a common root is
The values of k for which the quadratic equation \[k x^2 + 1 = kx + 3x - 11 x^2\] has real and equal roots are
If the equations \[x^2 + 2x + 3\lambda = 0 \text { and } 2 x^2 + 3x + 5\lambda = 0\] have a non-zero common roots, then λ =
The set of all values of m for which both the roots of the equation \[x^2 - (m + 1)x + m + 4 = 0\] are real and negative, is
If α and β are the roots of \[4 x^2 + 3x + 7 = 0\], then the value of \[\frac{1}{\alpha} + \frac{1}{\beta}\] is
If α, β are the roots of the equation \[x^2 - p(x + 1) - c = 0, \text { then } (\alpha + 1)(\beta + 1) =\]
Find the value of P such that the difference of the roots of the equation x2 – Px + 8 = 0 is 2.
Find the value of a such that the sum of the squares of the roots of the equation x2 – (a – 2)x – (a + 1) = 0 is least.
If `|(z - 2)/(z + 2)| = pi/6`, then the locus of z is ______.
