Question

The general solution of the differential equation \[\frac{dy}{dx} + y\] g' (x) = g (x) g' (x), where g (x) is a given function of x, is

Options

• g (x) + log {1 + y + g (x)} = C

• g (x) + log {1 + y − g (x)} = C

• g (x) − log {1 + y − g (x)} = C

• none of these

Answer 1

g (x) + log {1 + y − g (x)} = C

 

We have, 
\[\frac{dy}{dx} + y g'\left( x \right) = g\left( x \right)g'\left( x \right) . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form 
\[\frac{dy}{dx} + Py = Q\]
\[\text{ where }P = g'\left( x \right)\text{ and }Q = g\left( x \right)g'\left( x \right) . \]
\[ \therefore I . F . = e^{\int P\ dx} \]
\[ = e^{\int g'\left( x \right) dx} \]
\[ = e^{g\left( x \right)} \]
Multiplying both sides of (1) by I.F. , we get
\[ e^{g\left( x \right)} \left( \frac{dy}{dx} + yg'\left( x \right) \right) = e^{g\left( x \right)} g\left( x \right)g'\left( x \right)\]
\[ \Rightarrow e^{g\left( x \right)} \frac{dy}{dx} + e^{g\left( x \right)} y g'\left( x \right) = e^{g\left( x \right)} g\left( x \right)g'\left( x \right)\]
Integrating both sides with respect to x, we get
\[y e^{g\left( x \right)} = \int e^{g\left( x \right)} g\left( x \right)g'\left( x \right) dx + K\]
\[ \Rightarrow y e^{g\left( x \right)} = I + K\]
\[ \text{ where }I = \int e^{g\left( x \right)} g\left( x \right)g'\left( x \right) dx\]
Now,
\[I = \int e^{g\left( x \right)} g\left( x \right)g'\left( x \right) dx\]
\[\text{Putting }g\left( x \right) = t, \text{ we get }\]
\[g'\left( x \right) dx = dt\]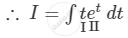

\[ = t\int e^t dt - \int\left[ \frac{d}{dx}\left( t \right)\int e^t dt \right]dt\]
\[ = t e^t - e^t \]
\[ = g\left( x \right) e^{g\left( x \right)} - e^{g\left( x \right)} \]
\[ \therefore y e^{g\left( x \right)} = g\left( x \right) e^{g\left( x \right)} - e^{g\left( x \right)} + K\]
\[ \Rightarrow y e^{g\left( x \right)} + e^{g\left( x \right)} - g\left( x \right) e^{g\left( x \right)} = K\]
\[ \Rightarrow y + 1 - g\left( x \right) = K e^{- g\left( x \right)} \]
Taking log on both sides, we get
\[\log\left\{ y + 1 - g\left( x \right) \right\} = - g\left( x \right) + \log K\]
\[ \Rightarrow g\left( x \right) + \log\left\{ 1 + y - g\left( x \right) \right\} = C ...........\left(\text{Where, }C = \log K \right)\]