Advertisements
Online Mock Tests
Chapters
![Samacheer Kalvi solutions for Business Mathematics and Statistics [English] Class 11 TN Board chapter 10 - Operations Research - Shaalaa.com](/images/business-mathematics-and-statistics-english-class-11-tn-board_6:5f2b1b2038084cf381bfa42c826a928c.jpg "Samacheer Kalvi solutions for Business Mathematics and Statistics [English] Class 11 TN Board chapter 10 - Operations Research")
Advertisements
Solutions for Chapter 10: Operations Research
Below listed, you can find solutions for Chapter 10 of Tamil Nadu Board of Secondary Education Samacheer Kalvi for Business Mathematics and Statistics [English] Class 11 TN Board.
Samacheer Kalvi solutions for Business Mathematics and Statistics [English] Class 11 TN Board 10 Operations Research Exercise 10.1 [Pages 243 - 244]
A company produces two types of pens A and B. Pen A is of superior quality and pen B is of lower quality. Profits on pens A and B are ₹ 5 and ₹ 3 per pen respectively. Raw materials required for each pen A is twice as that of pen B. The supply of raw material is sufficient only for 1000 pens per day. Pen A requires a special clip and only 400 such clips are available per day. For pen B, only 700 clips are available per day. Formulate this problem as a linear programming problem.
A company produces two types of products say type A and B. Profits on the two types of product are ₹ 30/- and ₹ 40/- per kg respectively. The data on resources required and availability of resources are given below.
| Requirements | Capacity available per month | ||
| Product A | Product B | ||
| Raw material (kgs) | 60 | 120 | 12000 |
| Machining hours/piece | 8 | 5 | 600 |
| Assembling (man hours) | 3 | 4 | 500 |
Formulate this problem as a linear programming problem to maximize the profit.
A company manufactures two models of voltage stabilizers viz., ordinary and auto-cut. All components of the stabilizers are purchased from outside sources, assembly and testing is carried out at the company’s own works. The assembly and testing time required for the two models are 0.8 hours each for ordinary and 1.20 hours each for auto-cut. Manufacturing capacity 720 hours at present is available per week. The market for the two models has been surveyed which suggests a maximum weekly sale of 600 units of ordinary and 400 units of auto-cut. Profit per unit for ordinary and auto-cut models has been estimated at ₹ 100 and ₹ 150 respectively. Formulate the linear programming problem.
Solve the following linear programming problems by graphical method.
Maximize Z = 6x1 + 8x2 subject to constraints 30x1 + 20x2 ≤ 300; 5x1 + 10x2 ≤ 110; and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 22x1 + 18x2 subject to constraints 960x1 + 640x2 ≤ 15360; x1 + x2 ≤ 20 and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Minimize Z = 3x1 + 2x2 subject to the constraints 5x1 + x2 ≥ 10; x1 + x2 ≥ 6; x1 + 4x2 ≥ 12 and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 40x1 + 50x2 subject to constraints 3x1 + x2 ≤ 9; x1 + 2x2 ≤ 8 and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Maximize Z = 20x1 + 30x2 subject to constraints 3x1 + 3x2 ≤ 36; 5x1 + 2x2 ≤ 50; 2x1 + 6x2 ≤ 60 and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Minimize Z = 20x1 + 40x2 subject to the constraints 36x1 + 6x2 ≥ 108; 3x1 + 12x2 ≥ 36; 20x1 + 10x2 ≥ 100 and x1, x2 ≥ 0.
Samacheer Kalvi solutions for Business Mathematics and Statistics [English] Class 11 TN Board 10 Operations Research Exercise 10.2 [Pages 249 - 250]
Draw the network for the project whose activities with their relationships are given below:
Activities A, D, E can start simultaneously; B, C > A; G, F > D, C; H > E, F.
Draw the event oriented network for the following data:
| Events | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Immediate Predecessors | - | 1 | 1 | 2, 3 | 3 | 4, 5 | 5, 6 |
Construct the network for the projects consisting of various activities and their precedence relationships are as given below:
A, B, C can start simultaneously A < F, E; B < D, C; E, D < G
Construct the network for each the projects consisting of various activities and their precedence relationships are as given below:
| Activity | A | B | C | D | E | F | G | H | I | J | K |
| Immediate Predecessors | - | - | - | A | B | B | C | D | E | H, I | F, G |
Construct the network for the project whose activities are given below.
| Activity | 0 - 1 | 1 - 2 | 1 - 3 | 2 - 4 | 2 - 5 | 3 - 4 | 3 - 6 | 4 - 7 | 5 - 7 | 6 - 7 |
| Duration (in week) | 3 | 8 | 12 | 6 | 3 | 3 | 8 | 5 | 3 | 8 |
Calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity. Determine the critical path and the project completion time.
A project schedule has the following characteristics
| Activity | 1 - 2 | 1 - 3 | 2 - 4 | 3 - 4 | 3 - 5 | 4 - 9 | 5 - 6 | 5 - 7 | 6 - 8 | 7 - 8 | 8 - 10 | 9 - 10 |
| Time | 4 | 1 | 1 | 1 | 6 | 5 | 4 | 8 | 1 | 2 | 5 | 7 |
Construct the network and calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.
Draw the network and calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.
| Jobs | 1 - 2 | 1 - 3 | 2 - 4 | 3 - 4 | 3 - 5 | 4 - 5 | 4 - 6 | 5 - 6 |
| Duration | 6 | 5 | 10 | 3 | 4 | 6 | 2 | 9 |
The following table gives the activities of a project and their duration in days
| Activity | 1 - 2 | 1 - 3 | 2 - 3 | 2 - 4 | 3 - 4 | 3 - 5 | 4 - 5 |
| Duration | 5 | 8 | 6 | 7 | 5 | 4 | 8 |
Construct the network and calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.
A Project has the following time schedule
| Activity | 1 - 2 | 1 - 6 | 2 - 3 | 2 - 4 | 3 - 5 | 4 - 5 | 6 - 7 | 5 - 8 | 7 - 8 |
| Duration (in days) | 7 | 6 | 14 | 5 | 11 | 7 | 11 | 4 | 18 |
Construct the network and calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and determine the Critical path of the project and duration to complete the project.
The following table use the activities in a construction projects and relevant information
| Activity | 1 - 2 | 1 - 3 | 2 - 3 | 2 - 4 | 3 - 4 | 4 - 5 |
| Duration (in days) |
22 | 27 | 12 | 14 | 6 | 12 |
Draw the network for the project, calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and find the critical path. Compute the project duration.
Samacheer Kalvi solutions for Business Mathematics and Statistics [English] Class 11 TN Board 10 Operations Research Exercise 10.3 [Pages 250 - 251]
Choose the correct answer
The critical path of the following network is
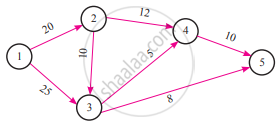
1 - 2 - 4 - 5
1 - 3 - 5
1 - 2 - 3 - 5
1 - 2 - 3 - 4 - 5
Maximize: z = 3x1 + 4x2 subject to 2x1 + x2 ≤ 40, 2x1 + 5x2 ≤ 180, x1, x2 ≥ 0. In the LPP, which one of the following is feasible comer point?
x1 = 18, x2 = 24
x1 = 15, x2 = 30
x1 = 2.5, x2 = 35
x1 = 20.5, x2 = 19
One of the conditions for the activity (i, j) to lie on the critical path is
Ej – Ei = Lj – Li = tij
Ei – Ej = Lj – Li = tij
Ej – Ei = Li – Lj = tij
Ej – Ei = Lj – Li ≠ tij
In constructing the network which one of the following statements is false?
Each activity is represented by one and only one arrow. (i.e.) only one activity can connect any two nodes.
Two activities can be identified by the same head and tail events.
Nodes are numbered to identify an activity uniquely. Tail node (starting point) should be lower than the head node (end point) of an activity.
Arrows should not cross each other.
In a network while numbering the events which one of the following statements is false?
Event numbers should be unique.
Event numbering should be carried out on a sequential basis from left to right.
The initial event is numbered 0 or 1.
The head of an arrow should always bear a number lesser than the one assigned at the tail of the arrow.
A solution which maximizes or minimizes the given LPP is called
a solution
a feasible solution
an optimal solution
none of these
In the given graph the coordinates of M1 are
x1 = 5, x2 = 30
x1 = 20, x2 = 16
x1 = 10, x2 = 20
x1 = 20, x2 = 30
The maximum value of the objective function Z = 3x + 5y subject to the constraints x ≥ 0, y ≥ 0 and 2x + 5y ≤ 10 is
6
15
25
31
The minimum value of the objective function Z = x + 3y subject to the constraints 2x + y ≤ 20, x + 2y ≤ 20, x > 0 and y > 0 is
10
20
0
5
Which of the following is not correct?
Objective that we aim to maximize or minimize
Constraints that we need to specify
Decision variables that we need to determine
Decision variables are to be unrestricted.
In the context of network, which of the following is not correct
A network is a graphical representation.
A project network cannot have multiple initial and final nodes
An arrow diagram is essentially a closed network
An arrow representing an activity may not have a length and shape
The objective of network analysis is to
Minimize total project cost
Minimize total project duration
Minimize production delays, interruption and conflicts
All the above
Network problems have the advantage in terms of project
Scheduling
Planning
Controlling
All the above
In critical path analysis, the word CPM mean
Critical path method
Crash project management
Critical project management
Critical path management
Given an L.P.P maximize Z = 2x1 + 3x2 subject to the constrains x1 + x2 ≤ 1, 5x1 + 5x2 ≥ 0 and x1 ≥ 0, x2 ≥ 0 using graphical method, we observe
No feasible solution
unique optimum solution
multiple optimum solution
none of these
Samacheer Kalvi solutions for Business Mathematics and Statistics [English] Class 11 TN Board 10 Operations Research Miscellaneous Problems [Page 252]
A firm manufactures two products A and B on which the profits earned per unit are ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. Product A requires one minute of processing time on M1 and two minutes on M2, While B requires one minute on M1 and one minute on M2. Machine M1 is available for not more than 7 hrs 30 minutes while M2 is available for 10 hrs during any working day. Formulate this problem as a linear programming problem to maximize the profit.
A firm manufactures pills in two sizes A and B. Size A contains 2 mgs of aspirin, 5 mgs of bicarbonate and 1 mg of codeine. Size B contains 1 mg. of aspirin, 8 mgs. of bicarbonate and 6 mgs. of codeine. It is found by users that it requires at least 12 mgs. of aspirin, 74 mgs. of bicarbonate and 24 mgs. of codeine for providing immediate relief. It is required to determine the least number of pills a patient should take to get immediate relief. Formulate the problem as a standard LLP.
Solve the following linear programming problem graphically.
Maximise Z = 4x1 + x2 subject to the constraints x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1 ≥ 0, x2 ≥ 0.
Solve the following linear programming problem graphically.
Minimize Z = 200x1 + 500x2 subject to the constraints: x1 + 2x2 ≥ 10; 3x1 + 4x2 ≤ 24 and x1 ≥ 0, x2 ≥ 0.
Solve the following linear programming problem graphically.
Maximize Z = 3x1 + 5x2 subject to the constraints: x1 + x2 ≤ 6, x1 ≤ 4; x2 ≤ 5, and x1, x2 ≥ 0.
Solve the following linear programming problem graphically.
Maximize Z = 60x1 + 15x2 subject to the constraints: x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1, x2 ≥ 0.
Draw a network diagram for the following activities.
| Activity code | A | B | C | D | E | F | G | H | I | J | K |
| Predecessor activity | - | A | A | A | B | C | C | C, D | E, F | G, H | I, J |
Draw the network diagram for the following activities.
| Activity code | A | B | C | D | E | F | G |
| Predecessor activity | - | - | A | A | B | C | D, E |
A Project has the following time schedule
| Activity | 1 - 2 | 2 - 3 | 2 - 4 | 3 - 5 | 4 - 6 | 5 - 6 |
| Duration (in days) |
6 | 8 | 4 | 9 | 2 | 7 |
Draw the network for the project, calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and find the critical path. Compute the project duration.
The following table gives the characteristics of the project
| Activity | 1 - 2 | 1 - 3 | 2 - 3 | 3 - 4 | 3 - 5 | 4 - 6 | 5 - 6 | 6 - 7 |
| Duration (in days) |
5 | 10 | 3 | 4 | 6 | 6 | 5 | 5 |
Draw the network for the project, calculate the earliest start time, earliest finish time, latest start time and latest finish time of each activity and find the critical path. Compute the project duration.
Solutions for 10: Operations Research
Samacheer Kalvi solutions for Business Mathematics and Statistics [English] Class 11 TN Board chapter 10 - Operations Research
Shaalaa.com has the Tamil Nadu Board of Secondary Education Mathematics Business Mathematics and Statistics [English] Class 11 TN Board Tamil Nadu Board of Secondary Education solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Samacheer Kalvi solutions for Mathematics Business Mathematics and Statistics [English] Class 11 TN Board Tamil Nadu Board of Secondary Education 10 (Operations Research) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Samacheer Kalvi textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Business Mathematics and Statistics [English] Class 11 TN Board chapter 10 Operations Research are Linear Programming Problem (L.P.P.), Network Analysis.
Using Samacheer Kalvi Business Mathematics and Statistics [English] Class 11 TN Board solutions Operations Research exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Samacheer Kalvi Solutions are essential questions that can be asked in the final exam. Maximum Tamil Nadu Board of Secondary Education Business Mathematics and Statistics [English] Class 11 TN Board students prefer Samacheer Kalvi Textbook Solutions to score more in exams.
Get the free view of Chapter 10, Operations Research Business Mathematics and Statistics [English] Class 11 TN Board additional questions for Mathematics Business Mathematics and Statistics [English] Class 11 TN Board Tamil Nadu Board of Secondary Education, and you can use Shaalaa.com to keep it handy for your exam preparation.
