Advertisements
Advertisements
प्रश्न
\[\frac{dy}{dx} + y = 4x\]
उत्तर
We have,
\[\frac{dy}{dx} + y = 4x . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dy}{dx} + Py = Q\]
\[\text{where }P = 1\text{ and }Q = 4x\]
\[ \therefore I . F . = e^{\int P\ dx} \]
\[ = e^{\int dx} \]
\[ = e^x \]
\[\text{Multiplying both sides of (1) by }I . F . = e^x,\text{ we get}\]
\[ e^x \left( \frac{dy}{dx} + y \right) = e^x 4x \]
\[ \Rightarrow e^x \frac{dy}{dx} + e^x y = e^x 4x\]
Integrating both sides with respect to x, we get
\[y e^x = 4\int x e^x dx + C\]
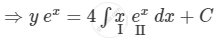
\[ \Rightarrow y e^x = 4x\int e^x dx - 4\int\left[ \frac{d}{dx}\left( x \right)\int e^x dx \right]dx + C\]
\[ \Rightarrow y e^x = 4x e^x - 4\int e^x dx + C\]
\[ \Rightarrow y e^x = 4x e^x - 4 e^x + C\]
\[ \Rightarrow y e^x = 4\left( x - 1 \right) e^x + C\]
\[ \Rightarrow y = 4\left( x - 1 \right) + C e^{- x} \]
\[\text{Hence, }y = 4\left( x - 1 \right) + C e^{- x}\text{ is the required solution.}\]
APPEARS IN
संबंधित प्रश्न
The differential equation of the family of curves y=c1ex+c2e-x is......
(a)`(d^2y)/dx^2+y=0`
(b)`(d^2y)/dx^2-y=0`
(c)`(d^2y)/dx^2+1=0`
(d)`(d^2y)/dx^2-1=0`
Find the particular solution of the differential equation `e^xsqrt(1-y^2)dx+y/xdy=0` , given that y=1 when x=0
Form the differential equation of the family of circles in the second quadrant and touching the coordinate axes.
Find the differential equation representing the curve y = cx + c2.
The number of arbitrary constants in the general solution of a differential equation of fourth order are ______.
The number of arbitrary constants in the particular solution of a differential equation of third order are ______.
Find the general solution of the differential equation `dy/dx + sqrt((1-y^2)/(1-x^2)) = 0.`
Find the particular solution of the differential equation
`tan x * (dy)/(dx) = 2x tan x + x^2 - y`; `(tan x != 0)` given that y = 0 when `x = pi/2`
Solve the differential equation:
`e^(x/y)(1-x/y) + (1 + e^(x/y)) dx/dy = 0` when x = 0, y = 1
The general solution of the differential equation \[\frac{dy}{dx} = \frac{y}{x}\] is
The solution of the differential equation \[\frac{dy}{dx} + \frac{2y}{x} = 0\] with y(1) = 1 is given by
The solution of the differential equation \[\frac{dy}{dx} - ky = 0, y\left( 0 \right) = 1\] approaches to zero when x → ∞, if
The solution of the differential equation \[\frac{dy}{dx} = \frac{x^2 + xy + y^2}{x^2}\], is
Which of the following differential equations has y = x as one of its particular solution?
The general solution of the differential equation \[\frac{y dx - x dy}{y} = 0\], is
Find the general solution of the differential equation \[x \cos \left( \frac{y}{x} \right)\frac{dy}{dx} = y \cos\left( \frac{y}{x} \right) + x .\]
cos (x + y) dy = dx
\[\frac{dy}{dx} - y \cot x = cosec\ x\]
`y sec^2 x + (y + 7) tan x(dy)/(dx)=0`
\[y - x\frac{dy}{dx} = b\left( 1 + x^2 \frac{dy}{dx} \right)\]
\[\frac{dy}{dx} + 5y = \cos 4x\]
For the following differential equation, find the general solution:- `y log y dx − x dy = 0`
Solve the following differential equation:-
\[\frac{dy}{dx} + \frac{y}{x} = x^2\]
Solve the following differential equation:-
\[x \log x\frac{dy}{dx} + y = \frac{2}{x}\log x\]
Solve the differential equation : `("x"^2 + 3"xy" + "y"^2)d"x" - "x"^2 d"y" = 0 "given that" "y" = 0 "when" "x" = 1`.
Find the differential equation of all non-horizontal lines in a plane.
Solve: `2(y + 3) - xy "dy"/"dx"` = 0, given that y(1) = – 2.
Solution of differential equation xdy – ydx = 0 represents : ______.
Solution of `("d"y)/("d"x) - y` = 1, y(0) = 1 is given by ______.
The solution of the equation (2y – 1)dx – (2x + 3)dy = 0 is ______.
The solution of `("d"y)/("d"x) + y = "e"^-x`, y(0) = 0 is ______.
Which of the following is the general solution of `("d"^2y)/("d"x^2) - 2 ("d"y)/("d"x) + y` = 0?
General solution of `("d"y)/("d"x) + ytanx = secx` is ______.
Solution of the differential equation `("d"y)/("d"x) + y/x` = sec x is ______.
Find the general solution of the differential equation:
`log((dy)/(dx)) = ax + by`.
The differential equation of all parabolas that have origin as vertex and y-axis as axis of symmetry is ______.
Solve the differential equation:
`(xdy - ydx) ysin(y/x) = (ydx + xdy) xcos(y/x)`.
Find the particular solution satisfying the condition that y = π when x = 1.
