Advertisements
Advertisements
प्रश्न
find the value of :
3sin2 30° + 2tan2 60° - 5cos2 45°
उत्तर
3 sin2 30° + 2 tan2 60° – 5 cos2 45°
= `3(1/2)^2 +2(sqrt3)^2 – 5(1/sqrt2)^2`
= `(3)/(4)+6 –(5)/(2)`
= `(3 + 24 – 10)/(4)`
= `4(1)/(4)`
APPEARS IN
संबंधित प्रश्न
Evaluate the following in the simplest form: sin 60º cos 45º + cos 60º sin 45º
Evaluate the following:
`(5cos^2 60° + 4sec^2 30° - tan^2 45°)/(sin^2 30° + cos^2 30°)`
Evaluate the following:
`(sin 20^@)/(cos 70^@)`
Evaluate the following :
`(cot 40^@)/cos 35^@ - 1/2 [(cos 35^@)/(sin 55^@)]`
Evaluate the following :
cosec 31° − sec 59°
Express each one of the following in terms of trigonometric ratios of angles lying between 0° and 45°
cos 78° + sec 78°
If A, B, C are the interior angles of a triangle ABC, prove that
`tan ((C+A)/2) = cot B/2`
Prove the following
sin θ sin (90° − θ) − cos θ cos (90° − θ) = 0
Prove the following :
`(cos(90^@ - theta) sec(90^@ - theta)tan theta)/(cosec(90^@ - theta) sin(90^@ - theta) cot (90^@ - theta)) + tan (90^@ - theta)/cot theta = 2`
Evaluate: `4(sin^2 30 + cos^4 60^@) - 2/3 3[(sqrt(3/2))^2 . [1/sqrt2]^2] + 1/4 (sqrt3)^2`
Evaluate tan 35° tan 40° tan 50° tan 55°
Prove that:
sin 60° cos 30° + cos 60° . sin 30° = 1
Prove that:
sin 60° = 2 sin 30° cos 30°
find the value of: cos2 60° + sec2 30° + tan2 45°
Prove that:
cos 30° . cos 60° - sin 30° . sin 60° = 0
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratio: cos 45°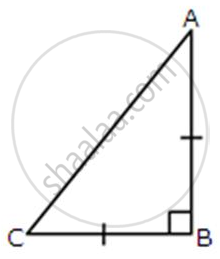
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratios: tan 45°
If sin x = cos y; write the relation between x and y, if both the angles x and y are acute.
If A = 30°;
show that:
4 cos A cos (60° - A). cos (60° + A) = cos 3A
Without using tables, evaluate the following: cosec330° cos60° tan345° sin290° sec245° cot30°.
Without using tables, find the value of the following: `(tan45°)/("cosec"30°) + (sec60°)/(cot45°) - (5sin90°)/(2cos0°)`
Prove that: `((cot30° + 1)/(cot30° -1))^2 = (sec30° + 1)/(sec30° - 1)`
Find the value of x in the following: `sqrt(3)sin x` = cos x
Find the value of x in the following: tan x = sin45° cos45° + sin30°
If A = 30° and B = 60°, verify that: sin (A + B) = sin A cos B + cos A sin B
If sin(A +B) = 1(A -B) = 1, find A and B.
If tan `"A" = (1)/(2), tan "B" = (1)/(3) and tan("A" + "B") = (tan"A" + tan"B")/(1 - tan"A" tan"B")`, find A + B.
Verify the following equalities:
1 + tan2 30° = sec2 30°
Find the value of x if `2 "cosec"^2 30 + x sin^2 60 - 3/4 tan^2 30` = 10
