Question

\[\frac{dy}{dx} = \frac{e^x \left( \sin^2 x + \sin 2x \right)}{y\left( 2 \log y + 1 \right)}\]

Answer 1

\[\frac{dy}{dx} = \frac{e^x \left( \sin^2 x + \sin 2x \right)}{y\left( 2\log y + 1 \right)}\]
\[ \Rightarrow y\left( 2\log y + 1 \right)dy = e^x \left( \sin^2 x + \sin 2x \right)dx\]
\[ \Rightarrow \left( 2y \log y + y \right)dy = \left( e^x \sin^2 x + e^x \sin 2x \right)dx\]
\[ \Rightarrow 2y \log y\ dy + y\ dy = e^x \sin^2 x dx + e^x \sin 2x dx\]
Integrating both sides, we get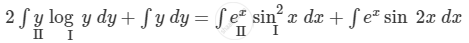

\[ \Rightarrow 2\left[ \log y\int y\ dy - \int\left\{ \frac{d}{dy}\left( \log y \right)\int y dy \right\} \right]dy + \int y dy = \sin^2 x\int e^x\ dx - \int\left[ \frac{d}{dx}\left( \sin^2 x \right)\int e^x dx \right]dx + \int e^x \sin 2x\ dx\]
\[ \Rightarrow 2\left[ \log y \left( \frac{y^2}{2} \right) - \int\left( \frac{1}{y} \right)\frac{y^2}{2}dy \right] + \int y\ dy = \sin^2 x e^x - \int\left[ 2\sin x\cos x e^x \right]dx + \int e^x \sin 2x\ dx + C\]
\[ \Rightarrow y^2 \log y - \int y\ dy + \int y\ dy = e^x \sin^2 x - \int e^x \sin 2x\ dx + \int e^x \sin 2x\ dx + C\]
\[ \Rightarrow y^2 \log y = e^x \sin^2 x + C\]