Advertisements
Advertisements
प्रश्न
In ∆ABC, cos C = `12/13` and BC = 24, then AC = ?
उत्तर
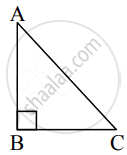
cos C = `12/13` .....(i) [Given]
In ∆ABC,
Let ∠ABC = 90°
∴ cos C = `"BC"/"AC"` .....(ii) [By definition]
∴ `"BC"/"AC" = 12/13` ......[From (i) and (ii)]
∴ `24/"AC" = 12/13`
∴ `(24 xx 13)/12` = AC
∴ `312/12` = AC
∴ AC = 26 units
संबंधित प्रश्न
If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A
Prove the following trigonometric identities.
(cosecθ + sinθ) (cosecθ − sinθ) = cot2 θ + cos2θ
if `tan theta = 1/sqrt2` find the value of `(cosec^2 theta - sec^2 theta)/(cosec^2 theta + cot^2 theta)`
if `tan theta = 3/4`, find the value of `(1 - cos theta)/(1 +cos theta)`
if `cot theta = sqrt3` find the value of `(cosec^2 theta + cot^2 theta)/(cosec^2 theta - sec^2 theta)`
Find the value of x, if sin x = sin 60° cos 30° – cos 60° sin 30°
Find the value of x, if tan x = `(tan60^circ - tan30^circ)/(1 + tan60^circ tan30^circ)`
Find the value of x, if cos (2x – 6) = cos2 30° – cos2 60°
Find the value of angle A, where 0° ≤ A ≤ 90°.
sin (90° – 3A) . cosec 42° = 1
Use tables to find cosine of 9° 23’ + 15° 54’
If A and B are complementary angles, prove that:
cosec2 A + cosec2 B = cosec2 A cosec2 B
∠ACD is an exterior angle of Δ ABC. If ∠B = 40o, ∠A = 70o find ∠ACD.
If θ is an acute angle such that sec2 θ = 3, then the value of \[\frac{\tan^2 \theta - {cosec}^2 \theta}{\tan^2 \theta + {cosec}^2 \theta}\]
The value of tan 10° tan 15° tan 75° tan 80° is
The value of
Solve: 2cos2θ + sin θ - 2 = 0.
If tan θ = cot 37°, then the value of θ is
The value of (tan1° tan2° tan3° ... tan89°) is ______.
`tan 47^circ/cot 43^circ` = 1
Prove the following:
tan θ + tan (90° – θ) = sec θ sec (90° – θ)
