Advertisements
Advertisements
प्रश्न
\[\frac{dy}{dx} = \frac{\sin x + x \cos x}{y\left( 2 \log y + 1 \right)}\]
Advertisements
उत्तर
We have,
\[\frac{dy}{dx} = \frac{\sin x + x \cos x}{y\left( 2 \log y + 1 \right)}\]
\[ \Rightarrow y \left( 2 \log y + 1 \right)dy = \left( \sin x + x \cos x \right)dx\]
Integrating both sides, we get
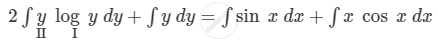
\[ \Rightarrow 2\log y\int y\ dy - 2\int\left( \frac{d}{dy}\left( \log y \right) \times \int y\ dy \right)dy + \int y\ dy = - \cos x + x\int \cos x\ dx - \int \left[ \frac{dx}{dx} \times \int\cos x \right] dx\]
\[ \Rightarrow y^2 \log y - \int y\ dy + \int y\ dy = - \cos x + x \sin x\ dx + \cos x + C\]
\[ \Rightarrow y^2 \log y = x \sin x + C\]
APPEARS IN
संबंधित प्रश्न
The solution of the differential equation dy/dx = sec x – y tan x is:
(A) y sec x = tan x + c
(B) y sec x + tan x = c
(C) sec x = y tan x + c
(D) sec x + y tan x = c
Find the particular solution of the differential equation `dy/dx=(xy)/(x^2+y^2)` given that y = 1, when x = 0.
Find the particular solution of the differential equation dy/dx=1 + x + y + xy, given that y = 0 when x = 1.
Verify that the given function (explicit or implicit) is a solution of the corresponding differential equation:
y = x2 + 2x + C : y′ – 2x – 2 = 0
Verify that the given function (explicit or implicit) is a solution of the corresponding differential equation:
y = x sin x : xy' = `y + x sqrt (x^2 - y^2)` (x ≠ 0 and x > y or x < -y)
Verify that the given function (explicit or implicit) is a solution of the corresponding differential equation:
`y = sqrt(a^2 - x^2 ) x in (-a,a) : x + y dy/dx = 0(y != 0)`
The number of arbitrary constants in the particular solution of a differential equation of third order are ______.
Show that the general solution of the differential equation `dy/dx + (y^2 + y +1)/(x^2 + x + 1) = 0` is given by (x + y + 1) = A (1 - x - y - 2xy), where A is parameter.
Solve the differential equation `[e^(-2sqrtx)/sqrtx - y/sqrtx] dx/dy = 1 (x != 0).`
Find a particular solution of the differential equation`(x + 1) dy/dx = 2e^(-y) - 1`, given that y = 0 when x = 0.
If y = etan x+ (log x)tan x then find dy/dx
The solution of the differential equation \[\frac{dy}{dx} = 1 + x + y^2 + x y^2 , y\left( 0 \right) = 0\] is
The number of arbitrary constants in the general solution of differential equation of fourth order is
The general solution of the differential equation \[\frac{y dx - x dy}{y} = 0\], is
The general solution of a differential equation of the type \[\frac{dx}{dy} + P_1 x = Q_1\] is
Find the general solution of the differential equation \[x \cos \left( \frac{y}{x} \right)\frac{dy}{dx} = y \cos\left( \frac{y}{x} \right) + x .\]
Find the particular solution of the differential equation \[\frac{dy}{dx} = \frac{x\left( 2 \log x + 1 \right)}{\sin y + y \cos y}\] given that
(x + y − 1) dy = (x + y) dx
\[\frac{dy}{dx} + y = 4x\]
`(dy)/(dx)+ y tan x = x^n cos x, n ne− 1`
Find the general solution of the differential equation \[\frac{dy}{dx} = \frac{x + 1}{2 - y}, y \neq 2\]
Find the particular solution of the differential equation \[\frac{dy}{dx} = - 4x y^2\] given that y = 1, when x = 0.
Solve the following differential equation:-
\[x\frac{dy}{dx} + 2y = x^2 , x \neq 0\]
Solve the following differential equation:-
\[\frac{dy}{dx} + 3y = e^{- 2x}\]
Find the equation of a curve passing through the point (0, 0) and whose differential equation is \[\frac{dy}{dx} = e^x \sin x.\]
Solve the differential equation: ` ("x" + 1) (d"y")/(d"x") = 2e^-"y" - 1; y(0) = 0.`
Solve the differential equation : `("x"^2 + 3"xy" + "y"^2)d"x" - "x"^2 d"y" = 0 "given that" "y" = 0 "when" "x" = 1`.
The solution of the differential equation `x "dt"/"dx" + 2y` = x2 is ______.
The general solution of the differential equation `"dy"/"dx" + y/x` = 1 is ______.
If y(t) is a solution of `(1 + "t")"dy"/"dt" - "t"y` = 1 and y(0) = – 1, then show that y(1) = `-1/2`.
Integrating factor of `(x"d"y)/("d"x) - y = x^4 - 3x` is ______.
The differential equation for which y = acosx + bsinx is a solution, is ______.
General solution of `("d"y)/("d"x) + ytanx = secx` is ______.
The solution of the differential equation ydx + (x + xy)dy = 0 is ______.
Find the general solution of the differential equation `x (dy)/(dx) = y(logy - logx + 1)`.
The curve passing through (0, 1) and satisfying `sin(dy/dx) = 1/2` is ______.
