Topics
Mathematics
Knowing Our Numbers
- Introduction to Knowing Our Numbers
- Comparing Numbers
- Compare Numbers in Ascending and Descending Order
- Compare Number by Forming Numbers from a Given Digits
- Compare Numbers by Shifting Digits
- Introducing a 5 Digit Number - 10,000
- Concept of Place Value
- Expansion Form of Numbers
- Introducing the Six Digit Number - 1,00,000
- Introducing seven-digit numbers
- Crores
- Using Commas in Indian and International Number System
- Round off and Estimation of Numbers
- To Estimate Sum Or Difference
- Estimating Products of Numbers
- Simplification of Expression by Using Brackets
- BODMAS - Rules for Simplifying an Expression
Whole Numbers
- Concept for Natural Numbers
- Concept for Whole Numbers
- Successor and Predecessor of Whole Number
- Operation of Whole Numbers on Number Line
- Properties of Whole Numbers
- Closure Property of Whole Number
- Associativity Property of Whole Numbers
- Division by Zero
- Commutativity Property of Whole Number
- Distributivity Property of Whole Numbers
- Identity of Addition and Multiplication of Whole Numbers
- Patterns in Whole Numbers
Playing with Numbers
- Arranging the Objects in Rows and Columns
- Factors and Multiples
- Concept of Perfect Number
- Concept of Prime Numbers
- Concept of Co-Prime Number
- Concept of Twin Prime Numbers
- Concept of Even and Odd Number
- Concept of Composite Number
- Eratosthenes’ method of finding prime numbers
- Tests for Divisibility of Numbers
- Divisibility by 10
- Divisibility by 5
- Divisibility by 2
- Divisibility by 3
- Divisibility by 6
- Divisibility by 4
- Divisibility by 8
- Divisibility by 9
- Divisibility by 11
- Common Factor
- Common Multiples
- Some More Divisibility Rules
- Prime Factorisation
- Highest Common Factor
- Lowest Common Multiple
Basic Geometrical Ideas
- Concept for Basic Geometrical Ideas (2 -d)
- Concept of Points
- Concept of Line
- Concept of Line Segment
- Concept of Ray
- Concept of Intersecting Lines
- Introduction to Parallel Lines
- Concept of Curves
- Different Types of Curves - Closed Curve, Open Curve, Simple Curve.
- Concept of Polygons
- Concept of Angle
- Concept of Triangles
- Concept of Quadrilaterals
- Concept of Circle
Understanding Elementary Shapes
- Introduction to Understanding Elementary Shapes
- Measuring Line Segments
- Right, Straight, and Complete Angle by Direction and Clock
- Concept of Angle
- Measuring Angles
- Perpendicular Line and Perpendicular Bisector
- Classification of Triangles (On the Basis of Sides, and of Angles)
- Classification of Triangles based on Sides- Equilateral, Isosceles, Scalene
- Classification of Triangles based on Angles: Acute-Angled, Right-Angled, Obtuse-Angled
- Types of Quadrilaterals
- Properties of a Square
- Properties of Rectangle
- Properties of a Parallelogram
- Properties of Rhombus
- Properties of Trapezium
- Three Dimensional Shapes
- Prism
- Concept of Pyramid
- Concept of Polygons
Integers
Fractions
Decimals
- The Decimal Number System
- Concept of Place Value
- Concept of Tenths, Hundredths and Thousandths in Decimal
- Representing Decimals on the Number Line
- Conversion between Decimal Fraction and Common Fraction
- Comparing Decimal Numbers
- Using Decimal Number as Units
- Addition of Decimal Fraction
- Subtraction of Decimal Fraction
Data Handling
Mensuration
Algebra
Ratio and Proportion
Symmetry
Practical Geometry
- Introduction to Geometric Tool
- Construction of a Circle When Its Radius is Known
- Construction of a Line Segment of a Given Length
- Constructing a Copy of a Given Line Segment
- Drawing a Perpendicular to a Line at a Point on the Line
- Drawing a perpendicular to a line from a point outside the line
- The Perpendicular Bisector
- Constructing an Angle of a Given Measure
- Construction of an angle bisector using a compass
- Concept of Angle Bisector
- Angles of Special Measures - 30°, 45°, 60°, 90°, and 120°
Notes
Angles of Special Measures:
There are some elegant and accurate methods to construct some angles of special sizes which do not require the use of the protractor.
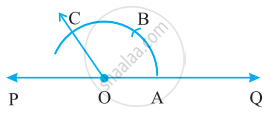
1. Constructing a 60° angle:
Step 1: Draw a line l and mark a point O on it.

Step 2: Place the pointer of the compasses at O and draw an arc of convenient radius which cuts the line `bar"PQ"` at a point say, A.

Step 3: With the pointer at A (as centre), now draw an arc that passes through O.

Step 4: Let the two arcs intersect at B. Join OB. We get ∠BOA whose measure is 60°.
2. Constructing a 30° angle:
To construct an angle of 30°, we need to draw an angle of 60° as above then bisect it with the process of an angle bisector.

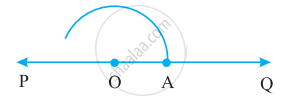
3. Constructing a 90° angle:
Step 1: Draw a line l and mark a point P on it. Now taking P as a centre and with a convenient radius, draw an arc of a circle which intersects line l at Q.
Step 2: Taking Q as a centre and with the same radius as before, draw an arc intersecting the previously drawn arc at R.
Step 3: Taking R as a centre and with the same radius as before, draw an arc intersecting the arc at S.
Step 4: Taking R and S as a centre, draw an arc of the same radius to intersect each other at T.
Step 5: Join PT, which is the required ray making 90° with line l.

4. Constructing a 45° angle:
Draw an angle of 90° then bisect it to make an angle of 45°.

5. Constructing a 120° angle:
An angle of 120° is nothing but twice of an angle of 60°.
Therefore, it can be constructed as follows :
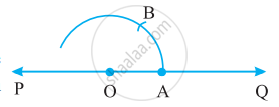
Step 1: Draw any line PQ and take a point O on it.

Step 2: Place the pointer of the compasses at O and draw an arc of convenient
radius which cuts the line at A.
Step 3: Without disturbing the radius on the compasses, draw an arc with A as the centre which cuts the first arc at B.
Step 4: Again without disturbing the radius on the compasses and with B as centre, draw an arc which cuts the first arc at C.

Step 5: Join OC, ∠COA is the required angle whose measure is 120°.