Topics
Mathematics
Knowing Our Numbers
- Introduction to Knowing Our Numbers
- Comparing Numbers
- Compare Numbers in Ascending and Descending Order
- Compare Number by Forming Numbers from a Given Digits
- Compare Numbers by Shifting Digits
- Introducing a 5 Digit Number - 10,000
- Concept of Place Value
- Expansion Form of Numbers
- Introducing the Six Digit Number - 1,00,000
- Introducing seven-digit numbers
- Crores
- Using Commas in Indian and International Number System
- Round off and Estimation of Numbers
- To Estimate Sum Or Difference
- Estimating Products of Numbers
- Simplification of Expression by Using Brackets
- BODMAS - Rules for Simplifying an Expression
Whole Numbers
- Concept for Natural Numbers
- Concept for Whole Numbers
- Successor and Predecessor of Whole Number
- Operation of Whole Numbers on Number Line
- Properties of Whole Numbers
- Closure Property of Whole Number
- Associativity Property of Whole Numbers
- Division by Zero
- Commutativity Property of Whole Number
- Distributivity Property of Whole Numbers
- Identity of Addition and Multiplication of Whole Numbers
- Patterns in Whole Numbers
Playing with Numbers
- Arranging the Objects in Rows and Columns
- Factors and Multiples
- Concept of Perfect Number
- Concept of Prime Numbers
- Concept of Co-Prime Number
- Concept of Twin Prime Numbers
- Concept of Even and Odd Number
- Concept of Composite Number
- Eratosthenes’ method of finding prime numbers
- Tests for Divisibility of Numbers
- Divisibility by 10
- Divisibility by 5
- Divisibility by 2
- Divisibility by 3
- Divisibility by 6
- Divisibility by 4
- Divisibility by 8
- Divisibility by 9
- Divisibility by 11
- Common Factor
- Common Multiples
- Some More Divisibility Rules
- Prime Factorisation
- Highest Common Factor
- Lowest Common Multiple
Basic Geometrical Ideas
- Concept for Basic Geometrical Ideas (2 -d)
- Concept of Points
- Concept of Line
- Concept of Line Segment
- Concept of Ray
- Concept of Intersecting Lines
- Introduction to Parallel Lines
- Concept of Curves
- Different Types of Curves - Closed Curve, Open Curve, Simple Curve.
- Concept of Polygons
- Concept of Angle
- Concept of Triangles
- Concept of Quadrilaterals
- Concept of Circle
Understanding Elementary Shapes
- Introduction to Understanding Elementary Shapes
- Measuring Line Segments
- Right, Straight, and Complete Angle by Direction and Clock
- Concept of Angle
- Measuring Angles
- Perpendicular Line and Perpendicular Bisector
- Classification of Triangles (On the Basis of Sides, and of Angles)
- Classification of Triangles based on Sides- Equilateral, Isosceles, Scalene
- Classification of Triangles based on Angles: Acute-Angled, Right-Angled, Obtuse-Angled
- Types of Quadrilaterals
- Properties of a Square
- Properties of Rectangle
- Properties of a Parallelogram
- Properties of Rhombus
- Properties of Trapezium
- Three Dimensional Shapes
- Prism
- Concept of Pyramid
- Concept of Polygons
Integers
Fractions
Decimals
- The Decimal Number System
- Concept of Place Value
- Concept of Tenths, Hundredths and Thousandths in Decimal
- Representing Decimals on the Number Line
- Conversion between Decimal Fraction and Common Fraction
- Comparing Decimal Numbers
- Using Decimal Number as Units
- Addition of Decimal Fraction
- Subtraction of Decimal Fraction
Data Handling
Mensuration
Algebra
Ratio and Proportion
Symmetry
Practical Geometry
- Introduction to Geometric Tool
- Construction of a Circle When Its Radius is Known
- Construction of a Line Segment of a Given Length
- Constructing a Copy of a Given Line Segment
- Drawing a Perpendicular to a Line at a Point on the Line
- Drawing a perpendicular to a line from a point outside the line
- The Perpendicular Bisector
- Constructing an Angle of a Given Measure
- Construction of an angle bisector using a compass
- Concept of Angle Bisector
- Angles of Special Measures - 30°, 45°, 60°, 90°, and 120°
Notes
Prime Factorisation:
a) Prime Factorisation:
When a number is expressed as a product of its factors we say that the number has been factorised. Thus, when we write 56 = 8 × 7, we say that 56 has been factorised. This is one of the factorisations of 56. The others are:
|
56 = 2 × 28 = 2 × 2 × 14 = 2 × 2 × 2 × 7 |
56 = 4 × 14 = 2 × 2 × 14 = 2 × 2 × 2 × 7 |
56 = 7 × 8 = 7 × 2 × 4 = 7 × 2 × 2 × 2 |
56 = 8 × 7 = 2 × 4 × 7 = 2 × 2 × 2 × 7 |
In all the above factorisations of 56, we ultimately arrive at only one factorisation 2 × 2 × 2 × 7. In this factorisation the only factors 2 is a prime number. Such a factorisation of a number is called prime factorisation.
Let us check this for the number 36.

The prime factorisation of 36 is 2 × 2 × 3 × 3. i.e. the only prime factorisation of 36.
Factor Tree:
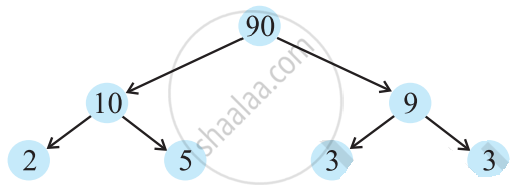
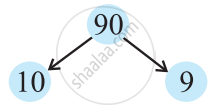
Consider the number 90.
Think of a factor pair say, 90 = 10 × 9.
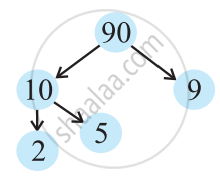
Now think of a factor pair of 10, 10 = 2 × 5.
Write factor pair of 99 = 3 × 3
b) Factorising a Number into its Prime Factors:
A simple but important rule given by Euclid is often used to find the GCD or HCF and LCM of numbers. The rule says that any composite number can be written as the product of prime numbers.
Let us learn how to find the prime factors of a number.
Example: Write the number 24 in the form of the product of its prime factors.
Method for finding prime factors
i) Vertical arrangement:
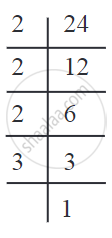
24 = 2 × 2 × 2 × 3
ii) Horizontal arrangement:
24 = 2 × 12
= 2 × 2 × 6...12 is factorised
= 2 × 2 × 2 × 3...6 is factorised.
The prime factors are 2 and 3.
Remember: To write a given number as a product of its prime factors is to factorise it into primes.
Example
Factorise into primes: 117.
Vertical arrangement:
| 3 | 117 |
| 3 | 39 |
| 13 | 13 |
| 1 |
117 = 3 × 3 × 13.
Horizontal arrangement:
117 = 13 × 9
117 = 13 × 3 × 3
117 = 3 × 3 × 13.
Example
Factorise into primes: 250.
Vertical arrangement:
| 2 | 250 |
| 5 | 125 |
| 5 | 25 |
| 5 | 5 |
| 1 |
250 = 2 × 5 × 5 × 5.
Horizontal arrangement:
250 = 2 × 125
250 = 2 × 5 × 25
250 = 2 × 5 × 5 × 5.
Example
Find the prime factors of 40.
Vertical arrangement:
| 2 | 40 |
| 2 | 20 |
| 2 | 10 |
| 5 | 5 |
| 1 |
40 = 2 × 2 × 2 × 5
Horizontal arrangement:
40 = 10 × 4
40 = 5 × 2 × 2 × 2.