Topics
Mathematics
Knowing Our Numbers
- Introduction to Knowing Our Numbers
- Comparing Numbers
- Compare Numbers in Ascending and Descending Order
- Compare Number by Forming Numbers from a Given Digits
- Compare Numbers by Shifting Digits
- Introducing a 5 Digit Number - 10,000
- Concept of Place Value
- Expansion Form of Numbers
- Introducing the Six Digit Number - 1,00,000
- Introducing seven-digit numbers
- Crores
- Using Commas in Indian and International Number System
- Round off and Estimation of Numbers
- To Estimate Sum Or Difference
- Estimating Products of Numbers
- Simplification of Expression by Using Brackets
- BODMAS - Rules for Simplifying an Expression
Whole Numbers
- Concept for Natural Numbers
- Concept for Whole Numbers
- Successor and Predecessor of Whole Number
- Operation of Whole Numbers on Number Line
- Properties of Whole Numbers
- Closure Property of Whole Number
- Associativity Property of Whole Numbers
- Division by Zero
- Commutativity Property of Whole Number
- Distributivity Property of Whole Numbers
- Identity of Addition and Multiplication of Whole Numbers
- Patterns in Whole Numbers
Playing with Numbers
- Arranging the Objects in Rows and Columns
- Factors and Multiples
- Concept of Perfect Number
- Concept of Prime Numbers
- Concept of Co-Prime Number
- Concept of Twin Prime Numbers
- Concept of Even and Odd Number
- Concept of Composite Number
- Eratosthenes’ method of finding prime numbers
- Tests for Divisibility of Numbers
- Divisibility by 10
- Divisibility by 5
- Divisibility by 2
- Divisibility by 3
- Divisibility by 6
- Divisibility by 4
- Divisibility by 8
- Divisibility by 9
- Divisibility by 11
- Common Factor
- Common Multiples
- Some More Divisibility Rules
- Prime Factorisation
- Highest Common Factor
- Lowest Common Multiple
Basic Geometrical Ideas
- Concept for Basic Geometrical Ideas (2 -d)
- Concept of Points
- Concept of Line
- Concept of Line Segment
- Concept of Ray
- Concept of Intersecting Lines
- Introduction to Parallel Lines
- Concept of Curves
- Different Types of Curves - Closed Curve, Open Curve, Simple Curve.
- Concept of Polygons
- Concept of Angle
- Concept of Triangles
- Concept of Quadrilaterals
- Concept of Circle
Understanding Elementary Shapes
- Introduction to Understanding Elementary Shapes
- Measuring Line Segments
- Right, Straight, and Complete Angle by Direction and Clock
- Concept of Angle
- Measuring Angles
- Perpendicular Line and Perpendicular Bisector
- Classification of Triangles (On the Basis of Sides, and of Angles)
- Classification of Triangles based on Sides- Equilateral, Isosceles, Scalene
- Classification of Triangles based on Angles: Acute-Angled, Right-Angled, Obtuse-Angled
- Types of Quadrilaterals
- Properties of a Square
- Properties of Rectangle
- Properties of a Parallelogram
- Properties of Rhombus
- Properties of Trapezium
- Three Dimensional Shapes
- Prism
- Concept of Pyramid
- Concept of Polygons
Integers
Fractions
Decimals
- The Decimal Number System
- Concept of Place Value
- Concept of Tenths, Hundredths and Thousandths in Decimal
- Representing Decimals on the Number Line
- Conversion between Decimal Fraction and Common Fraction
- Comparing Decimal Numbers
- Using Decimal Number as Units
- Addition of Decimal Fraction
- Subtraction of Decimal Fraction
Data Handling
Mensuration
Algebra
Ratio and Proportion
Symmetry
Practical Geometry
- Introduction to Geometric Tool
- Construction of a Circle When Its Radius is Known
- Construction of a Line Segment of a Given Length
- Constructing a Copy of a Given Line Segment
- Drawing a Perpendicular to a Line at a Point on the Line
- Drawing a perpendicular to a line from a point outside the line
- The Perpendicular Bisector
- Constructing an Angle of a Given Measure
- Construction of an angle bisector using a compass
- Concept of Angle Bisector
- Angles of Special Measures - 30°, 45°, 60°, 90°, and 120°
Notes
Highest Common Factor:
The Highest Common Factor(HCF) of two or more given numbers is the highest (or greatest) of their common factors. It is also known as Greatest Common Divisor (GCD).
a) HCF By Prime Factorization Method:
i) Find the HCF of 24 and 32 by the prime factors method.

24 = 4 × 6
= 2 × 2 × 2 × 3

32 = 8 × 4
= 2 × 2 × 2 × 2 × 2
The common factor 2 occurs thrice in each number. Therefore, the HCF = 2 × 2 × 2 = 8.
ii) Find the HCF of 195, 312, 546.
|
195 = 5 × 39 = 5 × 3 × 13 |
2 = 4 × 78 = 2 × 2 × 2 × 3 = 2 × 2 × 2 × 3 × 13 |
6 = 2 × 273 = 2 × 3 × 91 = 2 × 3 × 7 × 13 |
The common factors 3 and 13 each occur once in all the numbers.
∴ HCF = 3 × 13 = 39
iii) Find the HCF of 60, 12, 36
Let us work out this example in the vertical arrangement. We write all the numbers in one line and find their factors.

∴ HCF = 2 × 2 × 3 = 12
Note that 12 is a divisor of 36 and 60.
Note:
-
If one of the given numbers is a divisor of all the others, then it is the HCF of the given numbers.
-
If no prime number is a common divisor of all the given numbers, then 1 is their HCF because it is the only common divisor.
b) The Division Method for Finding the HCF:
i) Find the HCF of 144 and 252.

1. Divide the bigger number by the smaller one.
2. Divide the previous divisor by the remainder of this division.
3. Divide the divisor of step 2 by the remainder obtained in the division in step 2.
4. Continue like this till the remainder becomes zero. The divisor in the division in which the remainder is zero is the HCF of the given numbers.
∴ The HCF of 144 and 252 = 36.
ii) Reduce `(209)/(247)` to its simplest form.

To reduce the number to its simplest form, we will find the common factors of 209 and 247.
Let us find their HCF by the division method.
Here, 19 is the HCF. That is, the numerator and denominator are both divisible by 19.
∴ `(209)/(247) = (209 ÷ 19)/(247 ÷ 19) = 11/13`.
Example
Find the HCF of the following numbers: 20, 28, and 36.
The HCF of 20, 28 and 36 can also be found by prime factorisation of these numbers as follows:
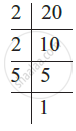
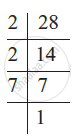
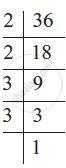
Thus,
20 = 2 × 2 × 5
28 = 2 × 2 × 7
36 = 2 × 2 × 3 × 3.
The common factor of 20, 28, and 36 is 2 (occurring twice).
Thus, HCF of 20, 28 and 36 is 2 × 2 = 4.
Example
Two tankers contain 850 litres and 680 litres of kerosene oil respectively. Find the maximum capacity of a container which can measure the kerosene oil of both the tankers when used an exact number of times.
The required container has to measure both the tankers in a way that a count is an exact number of times. So its capacity must be an exact divisor of the capacities of both the tankers. Moreover, this capacity should be maximum. Thus, the maximum capacity of such a container will be the HCF of 850 and 680.
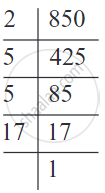

Hence,
850 = 2 × 5 × 5 × 17= 2 × 5 × 17 × 5 and
680 = 2 × 2 × 2 × 5 × 17= 2 × 5 × 17 × 2 × 2
The common factors of 850 and 680 are 2, 5 and 17.
Thus, the HCF of 850 and 680 is 2 × 5 × 17 = 170.
Therefore, the maximum capacity of the required container is 170 liters.
It will fill the first container in 5 and the second in 4 refills.
Example
There are 20 kg of jowar and 50 kg of wheat in a shop. All the grain is to be packed in bags. If all the bags are to have equal weights of grain, what is the maximum weight of grain that can be filled in each bag?
The weight of the grain in each bag must be a factor of 20 and 50.
Besides, the maximum possible weight must be filled in each bag. Hence, let us find the HCF of 20 and 50.
Factors of 20: 1, 2, 4, 5, 10, 20
Factors of 50: 1, 2, 5, 10, 25, 50
Common factors: 1, 2, 5, 10
Of the common factors of 20 and 50, 10 is the greatest, i.e. 10 is the HCF of the numbers 20 and 50.
Therefore, a maximum of 10 kg of grain can be filled in each bag.
Example
Find the HCF of 10, 15, 12.
10 = 2 × 5
15 = 3 × 5
12 = 2 × 2 × 3
No number except 1 is a common divisor.
Hence, HCF = 1.
Example
A shop sells a 450 g bottle of jam for 96 rupees and a bigger bottle of 600 g for 124 rupees. Which bottle is it more profitable to buy?
Let us use 150, the HCF of 450 and 600 to compare.
450 = 150 × 3, 600 = 150 × 4
∴ In the small bottle, 150 g of jam costs `96/3` = 32 rupees.
In the large bottle, 150 g of jam costs `(124)/4` = 31 rupees.
∴ Thus, it is more profitable to buy the 600 g bottle of jam.
