Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 12 TN Board chapter 9 - Applications of Integration [Latest edition]

Find an approximate value of `int_1^1.5` xdx by applying the left–end rule with the partition {1.1, 1.2, 1.3, 1.4, 1.5}

Find an approximate value of `int_1^1.5` x²dx by applying the right–end rule with the partition {1.1, 1.2, 1.3, 1.4, 1.5}

Find an approximate value of `int_1^1.5 (2 - x)` dx by applying the mid-point rule with the partition {1.1, 1.2, 1.3, 1.4, 1.5}

Evaluate the following integrals as the limits of sum:

`int_0^1 (5x + 4)"d"x`

Evaluate the following integrals as the limits of sum:

`int_1^2 (4x^2 - 1)"d"x`

Evaluate the following definite integrals:

`int_3^4 (d"x)/(x^2 - 4)`

Evaluate the following definite integrals:

`int_(-1)^1 ("d"x)/(x^2 + 2x + 5)`

Evaluate the following definite integrals:

`int_0^1 sqrt((1 - x)/(1 + x)) "d"x`

Evaluate the following definite integrals:

`int_0^(pi/2) "e"^x((1 + sin x)/(1 + cos x))"d"x`

Evaluate the following definite integrals:

`int_0^(pi/2) sqrt(cos theta) sin^3theta  "d"theta`

Evaluate the following definite integrals:

`int_0^1 (1 - x^2)/(1 + x^2)^2  "d"x`

Evaluate the following integrals using properties of integration:

`int_(-5)^5 x cos(("e"^x - 1)/("e"^x + 1))  "d"x`

Evaluate the following integrals using properties of integration:

`int_(- pi/2)^(pi/2) (x^5 + x cos x + tan^3 x + 1)  "d"x`

Evaluate the following integrals using properties of integration:

`int_(- pi/4)^(pi/4) sin^2x  "d"x`

Evaluate the following integrals using properties of integration:

`int_0^(2pi) x log((3 + cosx)/(3 - cosx)) "d"x`

Evaluate the following integrals using properties of integration:

`int_0^pi sin^4 x cos^3 x  "d"x`

Evaluate the following integrals using properties of integration:

`int_0^1 |5x - 3|  "d"x`

Evaluate the following integrals using properties of integration:

`int_0^(sin^2x) sin^-1 sqrt("t")  "dt" + int_0^(cos^2x) cos^-1 sqrt("t")  "dt"`

Evaluate the following integrals using properties of integration:

`int_0^1 (log(1 + x))/(1 + x^2)  "d"x`

Evaluate the following integrals using properties of integration:

`int_0^pi(xsinx)/(1 + sinx)  "'d"x`

Evaluate the following integrals using properties of integration:

`int_(pi/8)^((3pi)/8) 1/(1 + sqrt(tan x))  "d"x`

Evaluate the following integrals using properties of integration:

`int_0^pi x[sin^2(sin x) cos^2 (cos x)] "d"x`

Evaluate the following:

`int_0^1 x^3"e"^(-2x)  "d"x`

Evaluate the following:

`int_0^1 (sin(3tan^-1 x)tan^-1 x)/(1 + x^2)  "d"x`

Evaluate the following:

`int_0^(1/sqrt(2)) ("e"^(sin^-1x) sin^-1 x)/sqrt(1 - x^2)  "d"x`

Evaluate the following:

`int_0^(pi/2) x^2 cos 2x  "d"x`

Evaluate the following:

`int_0^(pi/2) ("d"x)/(1 + 5cos^2x)`

Evaluate the following:

`int_0^(pi/2) ("d"x)/(5 + 4sin^2x)`

Evaluate the following:

`int_0^(pi/2) sin^10 x  "d"x`

Evaluate the following:

`int_0^(pi/2) cos^7 x  "d"x`

Evaluate the following:

`int_0^(pi/4) sin^6 2x  "d"x`

Evaluate the following:

`int_0^(pi/6) sin^5 3x  "d"x`

Evaluate the following:

`int_0^(pi/2) sin^2x cos^4 x  "d"x`

Evaluate the following:

`int_0^(2pi) sin^7  x/4  "d"x`

Evaluate the following:

`int_0^(pi/2) sin^3theta cos^5theta  "d"theta`

Evaluate the following:

`int_1^0 x^2 (1 - x)^3  "d"x`

Evaluate the following:

`int_0^oo x^5 "e"^(-3x)  "d"x`

Evaluate the following:

`int_0^(pi/2) ("e"^(-tanx))/(cos^6x)  "d"x`

Evaluate the following:

If `int_0^oo "e"^(-"a"x^2) x^3  "d"x` = 32, `alpha > 0`, find `alpha`

Find the area of the region bounded by 3x – 2y + 6 = 0, x = – 3, x = 1 and x-axis

Find the area of the region bounded by 2x – y + 1 = 0, y = – 1, y = 3 and y-axis

Find the area of the region bounded by the curve 2 + x – x² + y = 0, x axis, x = – 3 and x = 3

Find the area of the region bounded by the line y = 2x + 5 and the parabola y = x² – 2x

Find the area of the region bounded between the curves y = sin x and y = cos x and the lines x = 0 and x = π

Find the area of the region bounded by y = tan x, y = cot x and the lines x = 0, x = `pi/2`, y = 0

Find the area of the region bounded by the parabola y² = x and the line y = x – 2

Father of a family wishes to divide his square field bounded by x = 0, x = 4, y = 4 and y = 0 along the curve y² = 4x and x² = 4y into three equal parts for his wife, daughter and son. Is it possible to divide? If so, find the area to be divided among them

The curve y = (x – 2)² + 1 has a minimum point at P. A point Q on the curve is such that the slope of PQ is 2. Find the area bounded by the curve and the chord PQ

Find the area of the region common to the circle x² + y² = 16 and the parabola y² = 6x

Find by integration, the volume of the solid generated by revolving about the x-axis, the region enclosed by y = 2x², y = 0 and x = 1

Find, by integration, the volume of the solid generated by revolving about the x axis, the region enclosed by y = e^-2x, y = 0, x = 0 and x = 1

Find, by integration, the volume of the solid generated by revolving about the y axis, the region enclosed by x² = 1 + y and y = 3

The region enclosed between the graphs of y = x and y = x² is denoted by R. Find the volume generated when R is rotated through 360° about x-axis

Find, by integration, the volume of the container which is in the shape of a right circular conical frustum as shown in the Fig 9.46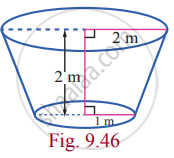

A watermelon has an ellipsoid shape which can be obtained by revolving an ellipse with major-axis 20 cm and minor-axis 10 cm about its major-axis. Find its volume using integration

Choose the correct alternative:

The value of `int_0^(2/3) ("d"x)/sqrt(4 - 9x^2)` is

Choose the correct alternative:

The value of `int_(-1)^2 |x|  "d"x` is

Choose the correct alternative:

For any value of n ∈ Z, `int_0^pi "e"^(cos^2x) cos^3[(2n+ 1)x]  "d"x` is

Choose the correct alternative:

The value of `int_(- pi/2)^(pi/2) sin^2x cos x  "d"x` is

Choose the correct alternative:

The value of `int_(-4)^4 [tan^-1  ((x^2)/(x^4 + 1)) + tan^-1 ((x^4 + 1)/x^2)] "d"x` is

Choose the correct alternative:

The value of `int_(- pi/4)^(pi/4) ((2x^7 - 3x^5 + 7x^3 - x + 1)/(cos^2x)) "d"x` is

Choose the correct alternative:

If `f(x) = int_0^x "t" cos  "t"  "dt"`, then `("d"f)/("d"x)` =

Choose the correct alternative:

The area between y² = 4x and its latus rectum is

Choose the correct alternative:

The value of `int_0^1 x(1 - x)^99  "d"x` is

Choose the correct alternative:

The value of `int_0^pi ("d"x)/(1 + 5^(cosx))` is

Choose the correct alternative:

If `("I'"("n" + 2))/("I'n")` = 90 then n is

Choose the correct alternative:

The value of `int_0^(pi/6) cos^3 3x  "d"x` is

Choose the correct alternative:

The value of  `int_10^pi sin^4x  "d"x`

Choose the correct alternative:

The value of `int_0^oo "e"^(-3x) x^2  "d"x` is

Choose the correct alternative:

If `int_0^"a" 1/(4 + x^2)  "dx=pi/8` then a is

Choose the correct alternative:

The volume of solid of revolution of the region bounded by y² = x(a – x) about the x-axis is

Choose the correct alternative:

If `f(x) = int_1^x "e"^(sin u)/u  "d"u, x > 1` and `int_1^3 "e"^(sin x^2)/x  "d"x = 1/2 [f("a") - f(1)]`. then one of the possible value of a is

Choose the correct alternative:

The value of `int_0^1 (sin^-1x)^2  "d"x` is

Choose the correct alternative:

The value of `int_0^"a" (sqrt("a"^2 - x^2))^3  "d"x` is

Choose the correct alternative:

If `int_0^x f("t")  "dt" = x + int_x^1 "t" f("t")  "dt"`, then the value of `f(1)` is