Question

Find the equation of the curve which passes through the point (1, 2) and the distance between the foot of the ordinate of the point of contact and the point of intersection of the tangent with x-axis is twice the abscissa of the point of contact.

Answer 1

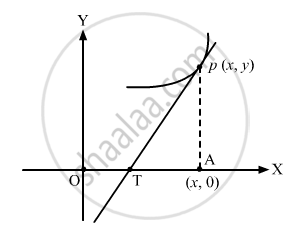
It is given that the distance between the foot of ordinate of point of contact (A) and point of intersection of tangent with x-axis (T) = 2x
\[\text{Coordinate of }T = \left( x - y\frac{dx}{dy}, 0 \right)\]

\[AT = \left[ x - \left( x - y \frac{dx}{dy} \right) \right] = 2x\]

\[\left[\text{Equation of tangent, }Y - y = \frac{dy}{dx}(X - x) \right]\]
\[\Rightarrow y - 0 = \frac{dy}{dx}\left(x - \left( x - y \frac{dx}{dy} \right) \right)\]
\[\Rightarrow y \frac{dx}{dy} = 2x\]
\[\Rightarrow \int\frac{dx}{x} = 2\int\frac{dy}{y}\]
\[\Rightarrow \ln x = \ln y^2 + \ln c\]
\[x = c y^2 \]
\[\text{As the circle passes through }\left( 1, 2 \right).\]
\[1 = c \times 2^2 \]
\[ \Rightarrow c = \frac{1}{4}\]
\[ \Rightarrow 4x = y^2\]