Advertisements
Advertisements
प्रश्न
Show that `2sin^-1(3/5) = tan^-1(24/7)`
उत्तर
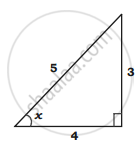
Let x = `sin^(-1)(3/5)`
sin x = `3/5`
tan x = `(3/4)`
x = `tan^(-1)(3/4)`
`sin^(-1)(3/5) = tan^(-1)(3/4)`
`2sin^(-1)(3/5) = 2tan^(-1)(3/4)`
= `tan^(-1)(3/4) + tan^(-1)(3/4)`
= `tan^(-1)(((3/4) + (3/4))/(1 - 3/4(3/4)))`
= `tan^(-1)((6/4)/(7/16))`
= `tan^(-1)(6/4 xx 16/7)`
= `tan^(-1)(24/7)`
`sin^(-1)(3/5) = tan^(-1)(24/7)`
APPEARS IN
संबंधित प्रश्न
Find the principal value of `cos^(-1) (sqrt3/2)`
Find the principal value of cosec−1 (2)
Find the principal value of `tan^(-1) (-sqrt3)`
Find the principal value of tan−1 (−1)
Find the value of the following:
`tan^(-1)(1) + cos^(-1) (-1/2) + sin^(-1) (-1/2)`
Find the value of the following:
`tan^(-1) (tan (7x)/6)`
`sin^-1 1/2-2sin^-1 1/sqrt2`
Evaluate the following:
`tan^-1 1+cos^-1 (-1/2)+sin^-1(-1/2)`
Find the set of values of `cosec^-1(sqrt3/2)`
Evaluate the following:
`\text(cosec)^-1(-2/sqrt3)+2cot^-1(-1)`
Evaluate: tan `[ 2 tan^-1 (1)/(2) – cot^-1 3]`
In ΔABC, if a = 18, b = 24, c = 30 then find the values of tan `A/2`
In ΔABC prove that `sin "A"/(2). sin "B"/(2). sin "C"/(2) = ["A(ΔABC)"]^2/"abcs"`
Find the principal value of the following: cosec- 1(2)
Find the principal value of the following: tan-1(– 1)
Find the principal value of the following: sin-1 `(1/sqrt(2))`
Find the principal value of the following: cos- 1`(-1/2)`
Prove the following:
`cos^-1(3/5) + cos^-1(4/5) = pi/(2)`
Prove the following:
`tan^-1(1/2) + tan^-1(1/3) = pi/(4)`
In ΔABC, prove the following:
`(cos A)/a + (cos B)/b + (cos C)/c = (a^2 + b^2 + c^2)/(2abc)`
Find the principal solutions of the following equation:
tan 5θ = -1
The principal value of sin−1`(1/2)` is ______
The principal value of cos−1`(-1/2)` is ______
If `sin(sin^-1(1/5) + cos^-1(x))` = 1, then x = ______
Evaluate cot(tan−1(2x) + cot−1(2x))
Evaluate `cos[pi/6 + cos^-1 (- sqrt(3)/2)]`
If tan−1x + tan−1y + tan−1z = π, then show that `1/(xy) + 1/(yz) + 1/(zx)` = 1
Prove that `2 tan^-1 (1/8) + tan^-1 (1/7) + 2tan^-1 (1/5) = pi/4`
Find the principal value of the following:
`sin^-1 (- 1/2)`
Find the principal value of the following:
cosec-1 (2)
Prove that:
2 tan-1 (x) = `sin^-1 ((2x)/(1 + x^2))`
Prove that `tan^-1 (m/n) - tan^-1 ((m - n)/(m + n)) = pi/4`
Express `tan^-1 [(cos x)/(1 - sin x)], - pi/2 < x < (3pi)/2` in the simplest form.
Express `tan^-1 ((cos x - sin x)/(cos x + sin x))`, 0 < x < π in the simplest form.
Find the principal value of `sin^-1 1/sqrt(2)`
Find the principal value of `sec^-1 (- sqrt(2))`
`sin^-1x + sin^-1 1/x + cos^-1x + cos^-1 1/x` = ______
In Δ ABC, with the usual notations, if sin B sin C = `"bc"/"a"^2`, then the triangle is ______.
sin[3 sin-1 (0.4)] = ______.
The principal value of `tan^{-1(sqrt3)}` is ______
`sin^2(sin^-1 1/2) + tan^2 (sec^-1 2) + cot^2(cosec^-1 4)` = ______.
The principal value of `sin^-1 (sin (3pi)/4)` is ______.
`cos(2sin^-1 3/4+cos^-1 3/4)=` ______.
If `tan^-1x + tan^-1y = (4pi)/5`, then `cot^-1x + cot^-1y` equals ______.
The value of `sin^-1(cos (53pi)/5)` is ______
`sin{tan^-1((1 - x^2)/(2x)) + cos^-1((1 - x^2)/(1 + x^2))}` is equal to ______
The domain of y = cos–1(x2 – 4) is ______.
The equation tan–1x – cot–1x = `(1/sqrt(3))` has ______.
Show that `cos(2tan^-1 1/7) = sin(4tan^-1 1/3)`
Prove that `tan^-1 1/4 + tan^-1 2/9 = sin^-1 1/sqrt(5)`
All trigonometric functions have inverse over their respective domains.
`"cos" 2 theta` is not equal to ____________.
When `"x" = "x"/2`, then tan x is ____________.
If `"x + y" = "x"/4` then (1+ tanx)(1 + tany) is equal to ____________.
`"sin" 265° - "cos" 265°` is ____________.
If tan-1 3 + tan-1 x = tan-1 8, then x = ____________.
`"sin"^-1 (-1/2)`
`"tan"^-1 (sqrt3)`
`"sin"^-1 (1/sqrt2)`
If tan-1 (x – 1) + tan-1 x + tan-1 (x + 1) = tan-1 3x, then the values of x are ____________.
`"sin" ["cot"^-1 {"cos" ("tan"^-1 "x")}] =` ____________.
The range of sin-1 x + cos-1 x + tan-1 x is ____________.
Find the value of sec2 (tan-1 2) + cosec2 (cot-1 3) ____________.
The equation 2cos-1 x + sin-1 x `= (11pi)/6` has ____________.
If tan-1 x – tan-1 y = tan-1 A, then A is equal to ____________.
`sin[π/3 - sin^-1 (-1/2)]` is equal to:
`"cos"^-1 ("cos" ((7pi)/6))` is equal to ____________.
`"tan"^-1 sqrt3 - "sec"^-1 (-2)` is equal to ____________.
The equation of the tangent to the curve given by x = a sin3t, y = bcos3t at a point where t = `pi/2` is
If A = `[(cosx, sinx),(-sinx, cosx)]`, then A1 A–1 is
Which of the following functions is inverse of itself?
sin 6θ + sin 4θ + sin 2θ = 0, then θ =
If `sqrt(2)` sec θ + tan θ = 1, then the general value of θ is
If `(-1)/sqrt(2) ≤ x ≤ 1/sqrt(2)` then `sin^-1 (2xsqrt(1 - x^2))` is equal to
What is the value of `sin^-1(sin (3pi)/4)`?
What is the values of `cos^-1 (cos (7pi)/6)`
Assertion (A): The domain of the function sec–12x is `(-∞, - 1/2] ∪ pi/2, ∞)`
Reason (R): sec–1(–2) = `- pi/4`
If θ = `sin^-1((2x)/(1 + x^2)) + cos^-1((1 - x^2)/(1 + x^2))`, for `x ≥ 3/2` then the absolute value of `((cosθ + tanθ + 4)/secθ)` is ______.
Let x = sin–1(sin8) + cos–1(cos11) + tan–1(tan7), and x = k(π – 2.4) for an integer k, then the value of k is ______.
cos–1(cos10) is equal to ______.
`cot^-1(sqrt(cos α)) - tan^-1 (sqrt(cos α))` = x, then sin x = ______.
Number of values of x which lie in [0, 2π] and satisfy the equation
`(cos x/4 - 2sinx) sinx + (1 + sin x/4 - 2cosx)cosx` = 0
If ax + b (sec (tan–1 x)) = c and ay + b (sec.(tan–1 y)) = c, then `(x + y)/(1 - xy)` = ______.
If x ∈ R – {0}, then `tan^-1 ((sqrt(1 + x^2) + sqrt(1 - x^2))/(sqrt(1 + x^2) - sqrt(1 - x^2)))`
If tan–1 2x + tan–1 3x = `π/4`, then x = ______.
`(tan^-1 (sqrt(3)) - sec^-1(-2))/("cosec"^-1(-sqrt(2)) + cos^-1(-1/2))` is equal to ______.
Find the value of `cos(x/2)`, if tan x = `5/12` and x lies in third quadrant.
If sin–1x – cos–1x = `π/6`, then x = ______.
Solve for x:
5tan–1x + 3cot–1x = 2π
Find the value of `tan^-1(x/y) + tan^-1((y - x)/(y + x))`
