Advertisements
Advertisements
Question
Solution
\[Let I = \int\left( \frac{x^2 + x + 1}{x^2 - x + 1} \right)dx\]
\[\text{ Now }, \]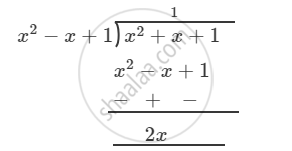
\[\text{ Therefore }, \]
\[\frac{x^2 + x + 1}{x^2 - x + 1} = 1 + \frac{2x}{x^2 - x + 1}\]
\[ \Rightarrow \int\left( \frac{x^2 + x + 1}{x^2 - x + 1} \right) dx = \int dx + \int\left( \frac{2x - 1 + 1}{x^2 - x + 1} \right) dx\]
\[ = \int dx + \int\left( \frac{2x - 1}{x^2 - x + 1} \right) dx + \int\frac{dx}{x^2 - x + 1}\]
\[ = \int dx + \int\frac{\left( 2x - 1 \right) dx}{x^2 - x + 1} + \int\frac{dx}{x^2 - x + \left( \frac{1}{2} \right)^2 - \left( \frac{1}{2} \right)^2 + 1}\]
\[ = \int dx + \int\frac{\left( 2x - 1 \right) dx}{x^2 - x + 1} + \int\frac{dx}{\left( x - \frac{1}{2} \right)^2 + \left( \frac{\sqrt{3}}{2} \right)^2}\]
\[ = x + \text{ log } \left| x^2 - x + 1 \right| + \frac{2}{\sqrt{3}} \text{ tan }^{- 1} \left( \frac{2x - 1}{\sqrt{3}} \right) + C\]
APPEARS IN
RELATED QUESTIONS
\[\int\sqrt{x}\left( 3 - 5x \right) dx\]
If f' (x) = 8x3 − 2x, f(2) = 8, find f(x)
If f' (x) = a sin x + b cos x and f' (0) = 4, f(0) = 3, f
` ∫ sin x \sqrt (1-cos 2x) dx `
\[\int\frac{x}{\sqrt{8 + x - x^2}} dx\]
Evaluate the following integral:
\[\int\frac{1}{\sqrt{x} + \sqrt{x + 1}} \text{ dx }\]
