Advertisements
Advertisements
प्रश्न
उत्तर
\[\text{ Let }I\int\left( \frac{x^2 + 1}{x^2 - 5x + 6} \right)dx\]
\[\text{Dividing Numerator by Denominator}\]
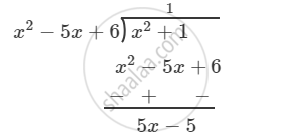
\[\frac{x^2 + 1}{x^2 - 5x + 6} = 1 + \left( \frac{5x - 5}{x^2 - 5x + 6} \right) . . . . . \left( 1 \right)\]
\[\text{ Also } \frac{5x - 5}{x^2 - 5x + 6} = \frac{5x - 5}{\left( x - 2 \right) \left( x - 3 \right)}\]
\[\text{ Let } \frac{5x - 5}{\left( x - 2 \right) \left( x - 3 \right)} = \frac{A}{x - 2} + \frac{B}{x - 3}\]
\[ \Rightarrow \frac{5x - 5}{\left( x - 2 \right) \left( x - 3 \right)} = \frac{A \left( x - 3 \right) + B \left( x - 2 \right)}{\left( x - 2 \right) \left( x - 3 \right)}\]
\[ \Rightarrow 5x - 5 = A \left( x - 3 \right) + B \left( x - 2 \right)\]
\[\text{ let } x = 3\]
\[5 \times 3 - 5 = A \times 0 + B \left( 3 - 2 \right)\]
\[10 = B\]
\[\text{ let } x = 2\]
\[5 \times 2 - 5 = A \left( 2 - 3 \right) + B \times 0\]
\[A = - 5\]
\[\frac{5x - 5}{\left( x - 2 \right) \left( x - 3 \right)} = \frac{- 5}{x - 2} + \frac{10}{x - 3} . . . . . \left( 2 \right)\]
\[\text{ from }\left( 1 \right) \text{ and }\left( 2 \right)\]
\[I = \int dx - 5\int\frac{dx}{x - 2} + 10\int\frac{dx}{x - 3}\]
\[ = x - 5 \text{ log } \left| x - 2 \right| + 10 \text{ log } \left| x - 3 \right| + C\]
APPEARS IN
संबंधित प्रश्न
` = ∫ root (3){ cos^2 x} sin x dx `
If \[\int\frac{\sin^8 x - \cos^8 x}{1 - 2 \sin^2 x \cos^2 x} dx\]
\[\int\frac{5 x^4 + 12 x^3 + 7 x^2}{x^2 + x} dx\]
