Advertisements
Advertisements
प्रश्न
Advertisements
उत्तर
\[\text{ Let } I = \int\frac{\left( x - 1 \right)^2}{x^2 + 2x + 2} dx\]
\[ = \int\left( \frac{x^2 - 2x + 1}{x^2 + 2x + 2} \right) dx\]
\[\text{ Here }, \]
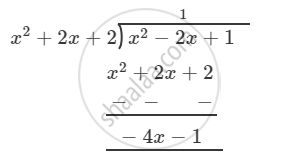
\[\text{ Thereforez }, \]
\[\frac{x^2 - 2x + 1}{x^2 + 2x + 2} = 1 - \frac{\left( 4x + 1 \right)}{x^2 + 2x + 2} . . . . . \left( 1 \right)\]
\[\text{ Let } 4x + 1 = A\frac{d}{dx} \left( x^2 + 2x + 2 \right) + B\]
\[4x + 1 = A \left( 2x + 2 \right) + B\]
\[4x + 1 = \left( 2A \right) x + 2A + B\]
\[ \text{ Equating Coefficients of like terms }\]
\[\text{ 2A = 4 }\]
\[A = 2\]
\[2A + B = 1\]
\[2 \times 2 + B = 1\]
\[B = - 3\]
\[\int\left( \frac{x^2 - 2x + 1}{x^2 + 2x + 2} \right) dx\]
\[ = \int dx - 2\int\frac{\left( 2x + 2 \right)}{x^2 + 2x + 2} dx + 3\int\frac{dx}{x^2 + 2x + 2}\]
\[ = \int dx - 2\int\frac{\left( 2x + 2 \right)}{x^2 + 2x + 2} dx + 3\int\frac{dx}{\left( x + 1 \right)^2 + 1^2}\]
\[ = x - 2 \text{ log } \left| x^2 + 2x + 2 \right| + \frac{3}{1} \tan^{- 1} \left( \frac{x + 1}{1} \right) + C\]
\[ = x - 2 \text { log } \left| x^2 + 2x + 2 \right| + 3 \tan^{- 1} \left( x + 1 \right) + C\]
APPEARS IN
संबंधित प्रश्न
` ∫ {sin 2x} /{a cos^2 x + b sin^2 x } ` dx
` ∫ e^{m sin ^-1 x}/ \sqrt{1-x^2} ` dx
Evaluate the following integrals:
The value of \[\int\frac{\sin x + \cos x}{\sqrt{1 - \sin 2x}} dx\] is equal to
\[\int\frac{x^3}{\sqrt{1 + x^2}}dx = a \left( 1 + x^2 \right)^\frac{3}{2} + b\sqrt{1 + x^2} + C\], then
\[\int\frac{1}{\sqrt{x} + \sqrt{x + 1}} \text{ dx }\]
\[\int\frac{x + 3}{\left( x + 4 \right)^2} e^x dx =\]
