Question

\[\int\frac{x^3 - 1}{x^3 + x} dx\]

Answer 1

We have,
\[I = \int \frac{\left( x^3 - 1 \right)dx}{x^3 + x}\]

Degree of numerator is equal to degree of denominator.
We divide numerator by denominator.

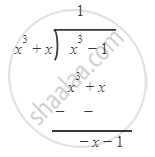
\[ \therefore \frac{x^3 - 1}{x^3 + x} = 1 - \frac{\left( x + 1 \right)}{x^3 + x}\]
\[ \Rightarrow \frac{x^3 - 1}{x^3 + x} = 1 - \frac{\left( x + 1 \right)}{x\left( x^2 + 1 \right)} . . . . . \left( 1 \right)\]
\[\text{Let }\frac{x + 1}{x\left( x^2 + 1 \right)} = \frac{A}{x} + \frac{Bx + C}{x^2 + 1}\]
\[ \Rightarrow \frac{x + 1}{x\left( x^2 + 1 \right)} = \frac{A\left( x^2 + 1 \right) + \left( Bx + C \right)\left( x \right)}{x\left( x^2 + 1 \right)}\]
\[ \Rightarrow x + 1 = A x^2 + A + B x^2 + Cx\]
\[ \Rightarrow x + 1 = \left( A + B \right) x^2 + Cx + A\]

Equating coefficient of like terms

A + B = 0
C = 1
A = 1
B = –1

\[\therefore \frac{x + 1}{x\left( x^2 + 1 \right)} = \frac{1}{x} + \frac{- x + 1}{x^2 + 1} . . . . . \left( 2 \right)\]
Using (1) and (2)
\[\int \frac{\left( x^3 - 1 \right)dx}{\left( x^3 + x \right)} = \int \left( 1 - \frac{1}{x} + \frac{x}{x^2 + 1} - \frac{1}{x^2 + 1} \right)dx\]
\[ = \int dx - \int\frac{dx}{x} + \int\frac{x dx}{x^2 + 1} - \int\frac{dx}{x^2 + 1} \]
\[\text{Putting }x^2 + 1 = t\]
\[ \Rightarrow 2x dx = dt\]
\[ \Rightarrow x dx = \frac{dt}{2}\]
\[ \therefore I = \int dx - \int\frac{dx}{x} + \frac{1}{2}\int\frac{dt}{t} - \int\frac{dx}{x^2 + 1}\]
\[ = x - \log \left| x \right| + \frac{1}{2}\log \left| t \right| - \tan^{- 1} x + C\]
\[ = x - \log \left| x \right| + \frac{1}{2}\log \left| x^2 + 1 \right| - \tan^{- 1} x + C\]