Advertisements
Advertisements
प्रश्न
उत्तर
We have,
\[I = \int \frac{\left( x^2 + 1 \right) \left( x^2 + 2 \right)}{\left( x^2 + 3 \right) \left( x^2 + 4 \right)}\]
\[\text{Putting }x^2 = t\]
Then,
\[\frac{\left( x^2 + 1 \right) \left( x^2 + 2 \right)}{\left( x^2 + 3 \right) \left( x^2 + 4 \right)} = \frac{\left( t + 1 \right) \left( t + 2 \right)}{\left( t + 3 \right) \left( t + 4 \right)} = \frac{t^2 + 3t + 2}{t^2 + 7t + 12}\]
Degree of numerator is equal to degree of denominator.
We divide numerator by denominator.
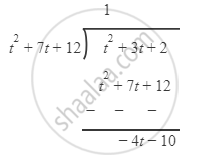
\[\therefore \frac{t^2 + 3t + 2}{t^2 + 7t + 12} = 1 - \left( \frac{4t + 10}{t^2 + 7t + 12} \right)\]
\[ \Rightarrow \frac{t^2 + 3t + 2}{t^2 + 7t + 12} = 1 - \frac{4t + 10}{\left( t + 3 \right) \left( t + 4 \right)} ............. \left( 1 \right)\]
\[\text{Let }\frac{4t + 10}{\left( t + 3 \right) \left( t + 4 \right)} = \frac{A}{t + 3} + \frac{B}{t + 4}\]
\[ \Rightarrow \frac{4t + 10}{\left( t + 3 \right) \left( t + 4 \right)} = \frac{A\left( t + 4 \right) + B\left( t + 3 \right)}{\left( t + 3 \right) \left( t + 4 \right)}\]
\[ \Rightarrow 4t + 10 = A\left( t + 4 \right) + B\left( t + 3 \right)\]
\[\text{Putting t + 4 = 0}\]
\[ \Rightarrow t = - 4\]
\[ \therefore - 16 + 10 = B\left( - 1 \right)\]
\[ \Rightarrow B = 6\]
\[\text{Putting t + 3 = 0}\]
\[ \Rightarrow t = - 3\]
\[ \therefore - 12 + 10 = A\left( - 3 + 4 \right)\]
\[ \Rightarrow A = - 2\]
\[ \therefore \frac{4t + 10}{\left( t + 3 \right) \left( t + 4 \right)} = \frac{- 2}{t + 3} + \frac{6}{t + 4} ................ \left( 2 \right)\]
From (1) and (2)
\[\frac{t^2 + 3t + 2}{t^2 + 7t + 12} = 1 + \frac{2}{t + 3} - \frac{6}{t + 4}\]
\[ \therefore \int\frac{\left( x^2 + 1 \right) \left( x^2 + 2 \right)dx}{\left( x^2 + 3 \right) \left( x^2 + 4 \right)} = \int dx + 2\int\frac{dx}{x^2 + \left( \sqrt{3} \right)^2} - 6\int\frac{dx}{x^2 + 2^2}\]
\[ = x + \frac{2}{\sqrt{3}} \tan^{- 1} \left( \frac{x}{\sqrt{3}} \right) - \frac{6}{2} \tan^{- 1} \left( \frac{x}{2} \right) + C\]
\[ = x + \frac{2}{\sqrt{3}} \tan^{- 1} \left( \frac{x}{\sqrt{3}} \right) - 3 \tan^{- 1} \left( \frac{x}{2} \right) + C\]
APPEARS IN
संबंधित प्रश्न
` = ∫1/{sin^3 x cos^ 2x} dx`
\[\int\frac{1}{2 + \cos x} \text{ dx }\]
