Question

\[\int\frac{x^2}{\left( x - 1 \right) \sqrt{x + 2}}\text{  dx}\]

Answer 1

\[\text{ We  have,} \]
\[I = \int \frac{x^2}{\left( x - 1 \right) \sqrt{x + 2}}\text{ dx }\]
\[\text{Putting  x }+ 2 = t^2 \]
\[x = t^2 - 2\]
\[\text{ Diff  both  sides }\]
\[dx = 2t \text{ dt }\]
\[I = \int \frac{\left( t^2 - 2 \right)^2}{\left( t^2 - 2 - 1 \right)t}2 \text{   t dt }\]
\[ = 2\int \frac{\left( t^2 - 2 \right)^2 dt}{t^2 - 3}\]
\[ = 2\int \frac{\left( t^4 - 4 t^2 + 4 \right)}{t^2 - 3}dt\]
\[\text{Dividing numerator by denominator, we get}\]

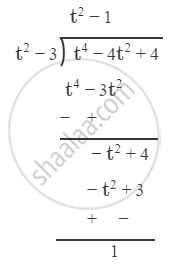
\[ \therefore I = 2\int\left( t^2 - 1 + \frac{1}{t^2 - 3} \right)dt \]
\[ = 2\int t^2 dt - 2\int dt + 2\int\frac{dt}{t^2 - \left( \sqrt{3} \right)^2}\]
\[ = 2\left[ \frac{t^3}{3} \right] - 2t + 2 \times \frac{1}{2\sqrt{3}}\text{ log }\left| \frac{t - \sqrt{3}}{t + \sqrt{3}} \right| + C\]
\[ = \frac{2}{3} \left( \sqrt{x + 2} \right)^3 - 2\sqrt{x + 2} + \frac{1}{\sqrt{3}}\text{ log} \left| \frac{\sqrt{x + 2} - \sqrt{3}}{\sqrt{x + 2} + \sqrt{3}} \right| + C\]
\[ = \frac{2}{3} \left( x + 2 \right)^\frac{3}{2} - 2\sqrt{x + 2} + \frac{1}{\sqrt{3}}\text{ log }\left| \frac{\sqrt{x + 2} - \sqrt{3}}{\sqrt{x + 2} + \sqrt{3}} \right| + C\]