Advertisements
Chapters
2: Compound Interest (Without using formula)
3: Compound Interest (Using Formula)
4: Expansions (Including Substitution)
5: Factorisation
6: Simultaneous (Linear) Equations (Including Problems)
7: Indices (Exponents)
8: Logarithms
9: Triangles [Congruency in Triangles]
10: Isosceles Triangles
11: Inequalities
12: Mid-point and Its Converse [ Including Intercept Theorem]
13: Pythagoras Theorem [Proof and Simple Applications with Converse]
14: Rectilinear Figures [Quadrilaterals: Parallelogram, Rectangle, Rhombus, Square and Trapezium]
15: Construction of Polygons (Using ruler and compass only)
16: Area Theorems [Proof and Use]
17: Circle
18: Statistics
19: Mean and Median (For Ungrouped Data Only)
20: Area and Perimeter of Plane Figures
21: Solids [Surface Area and Volume of 3-D Solids]
22: Trigonometrical Ratios [Sine, Consine, Tangent of an Angle and their Reciprocals]
▶ 23: Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios]
24: Solution of Right Triangles [Simple 2-D Problems Involving One Right-angled Triangle]
25: Complementary Angles
26: Co-ordinate Geometry
27: Graphical Solution (Solution of Simultaneous Linear Equations, Graphically)
28: Distance Formula
![Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 23 - Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios] Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 23 - Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios] - Shaalaa.com](/images/concise-mathematics-english-class-9-icse_6:b313c06da7fb4b0f885a06c3b5e4e4fa.jpg)
Advertisements
Solutions for Chapter 23: Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios]
Below listed, you can find solutions for Chapter 23 of CISCE Selina for Concise Mathematics [English] Class 9 ICSE.
Selina solutions for Concise Mathematics [English] Class 9 ICSE 23 Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios] Exercise 23 (A) [Pages 291 - 292]
find the value of: sin 30° cos 30°
find the value of: tan 30° tan 60°
find the value of: cos2 60° + sin2 30°
find the value of: cosec2 60° - tan2 30°
find the value of: sin2 30° + cos2 30°+ cot2 45°
find the value of: cos2 60° + sec2 30° + tan2 45°
Find the value of:
tan2 30° + tan2 45° + tan2 60°
find the value of :
`( tan 45°)/ (cos ec30°) +( sec60°)/(co 45°) – (5 sin 90°)/ (2 cos 0°)`
find the value of :
3sin2 30° + 2tan2 60° - 5cos2 45°
Prove that:
sin 60° cos 30° + cos 60° . sin 30° = 1
Prove that:
cos 30° . cos 60° - sin 30° . sin 60° = 0
Prove that:
cosec2 45° - cot2 45° = 1
Prove that:
cos2 30° - sin2 30° = cos 60°
Prove that:
`((tan60° + 1)/(tan 60° – 1))^2 = (1+ cos 30°) /(1– cos 30°) `
Prove that:
3 cosec2 60° - 2 cot2 30° + sec2 45° = 0
prove that:
sin (2 × 30°) = `(2 tan 30°)/(1+tan^2 30°)`
prove that:
cos (2 x 30°) = `(1 – tan^2 30°)/(1+tan^2 30°)`
prove that:
tan (2 x 30°) = `(2 tan 30°)/(1– tan^2 30°)`
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratios: sin 45°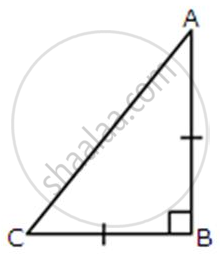
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratio: cos 45°
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratios: tan 45°
Prove that:
sin 60° = 2 sin 30° cos 30°
Prove that:
4 (sin4 30° + cos4 60°) -3 (cos2 45° - sin2 90°) = 2
If sin x = cos x and x is acute, state the value of x
If sec A = cosec A and 0° ∠A ∠90°, state the value of A
If tan θ = cot θ and 0°∠θ ∠90°, state the value of θ
If sin x = cos y; write the relation between x and y, if both the angles x and y are acute.
If sin x = cos y, then x + y = 45° ; write true of false
True
False
secθ . Cot θ= cosecθ ; write true or false
True
False
For any angle θ, state the value of: sin2 θ + cos2 θ
State for any acute angle θ whether sin θ increases or decreases as θ increases
Increases
Decreases
State for any acute angle θ whether cos θ increases or decreases as θ increases.
Increases
Decreases
State for any acute angle θ whether tan θ increases or decreases as θ decreases.
Increases
Decreases
If `sqrt3` = 1.732, find (correct to two decimal place) the value of sin 60o
If `sqrt3` = 1.732, find (correct to two decimal place) the value of `(2)/(tan 30°)`
Evaluate:
`(cos3"A" – 2cos4"A")/(sin3"A" + 2sin4"A")` , when A = 15°
Evaluate :
`(3 sin 3"B" + 2 cos(2"B" + 5°))/(2 cos 3"B" – sin (2"B" – 10°)` ; when "B" = 20°.
Selina solutions for Concise Mathematics [English] Class 9 ICSE 23 Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios] Exercise 23 (B) [Page 293]
Given A = 60° and B = 30°,
prove that : sin (A + B) = sin A cos B + cos A sin B
Given A = 60° and B = 30°,
prove that : cos (A + B) = cos A cos B - sin A sin B
Given A = 60° and B = 30°,
prove that : cos (A - B) = cos A cos B + sin A sin B
Given A = 60° and B = 30°,
prove that: tan (A - B) = `(tan"A" – tan"B")/(1 + tan"A".tan"B")`
If A =30o, then prove that :
sin 2A = 2sin A cos A = `(2 tan"A")/(1 + tan^2"A")`
If A =30o, then prove that :
cos 2A = cos2A - sin2A = `(1 – tan^2"A")/(1+ tan^2"A")`
If A = 30o, then prove that :
2 cos2 A - 1 = 1 - 2 sin2A
If A =30o, then prove that :
sin 3A = 3 sin A - 4 sin3A.
If A = B = 45° ,
show that:
sin (A - B) = sin A cos B - cos A sin B
If A = B = 45° ,
show that:
cos (A + B) = cos A cos B - sin A sin B
If A = 30°;
show that:
sin 3 A = 4 sin A sin (60° - A) sin (60° + A)
If A = 30°;
show that:
(sinA - cosA)2 = 1 - sin2A
If A = 30°;
show that:
cos 2A = cos4 A - sin4 A
If A = 30°;
show that:
`(1 – cos 2"A")/(sin 2"A") = tan"A"`
If A = 30°;
show that:
`(1 + sin 2"A" + cos 2"A")/(sin "A" + cos"A") = 2 cos "A"`
If A = 30°;
show that:
4 cos A cos (60° - A). cos (60° + A) = cos 3A
If A = 30°;
show that:
`(cos^3"A" – cos 3"A")/(cos "A") + (sin^3"A" + sin3"A")/(sin"A") = 3`
Selina solutions for Concise Mathematics [English] Class 9 ICSE 23 Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios] Exercise 23 (C) [Pages 297 - 298]
Solve the following equation for A, if 2 sin A = 1
Solve the following equation for A, if 2cos2A = 1
Solve the following equation for A, if sin 3 A = `sqrt3 /2`
Solve the following equation for A, if sec 2A = 2
Solve the following equations for A, if `sqrt3` tan A = 1
Solve the following equation for A, if tan 3 A = 1
Solve the following equation for A, if 2 sin 3 A = 1
Solve the following equation for A, if `sqrt3` cot 2 A = 1
Calculate the value of A, if (sin A - 1) (2 cos A - 1) = 0
Calculate the value of A, if (tan A - 1) (cosec 3A - 1) = 0
Calculate the value of A, if (sec 2A - 1) (cosec 3A - 1) = 0
Calculate the value of A, if cos 3A. (2 sin 2A - 1) = 0
Calculate the value of A, if (cosec 2A - 2) (cot 3A - 1) = 0
If 2 sin x° - 1 = 0 and x° is an acute angle; find:
- sin x°
- x°
- cos x° and tan x°.
If 4 cos2 x° - 1 = 0 and 0 ∠ x° ∠ 90°,
find:(i) x°
(ii) sin2 x° + cos2 x°
(iii) `(1)/(cos^2xx°) – (tan^2 xx°)`
If 4 sin2 θ - 1= 0 and angle θ is less than 90°, find the value of θ and hence the value of cos2 θ + tan2θ.
If sin 3A = 1 and 0 < A < 90°, find sin A
If sin 3A = 1 and 0 < A < 90°, find cos 2A
If sin 3A = 1 and 0 < A < 90°, find `tan^2A - (1)/(cos^2 "A")`
If 2 cos 2A = `sqrt3` and A is acute,
find:
(i) A
(ii) sin 3A
(iii) sin2 (75° - A) + cos2 (45° +A)
If sin x + cos y = 1 and x = 30°, find the value of y
If 3 tan A - 5 cos B = `sqrt3` and B = 90°, find the value of A
From the given figure,
find:
(i) cos x°
(ii) x°
(iii) `(1)/(tan^2 xx°) – (1)/(sin^2xx°)`
(iv) Use tan xo, to find the value of y.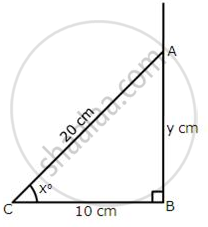
Use the given figure to find:
(i) tan θ°
(ii) θ°
(iii) sin2θ° - cos2θ°
(iv) Use sin θ° to find the value of x.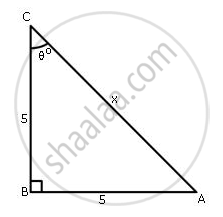
Find the magnitude of angle A, if 2 sin A cos A - cos A - 2 sin A + 1 = 0
Find the magnitude of angle A, if tan A - 2 cos A tan A + 2 cos A - 1 = 0
Find the magnitude of angle A, if 2 cos2 A - 3 cos A + 1 = 0
Find the magnitude of angle A, if 2 tan 3A cos 3A - tan 3A + 1 = 2 cos 3A
Solve for x : 2 cos 3x - 1 = 0
Solve for x : cos `(x)/(3) –1` = 0
Solve for x : sin (x + 10°) = `(1)/(2)`
Solve for x : cos (2x - 30°) = 0
Solve for x : 2 cos (3x - 15°) = 1
Solve for x : tan2 (x - 5°) = 3
Solve for x : 3 tan2 (2x - 20°) = 1
Solve for x : cos `(x/(2)+10°) = (sqrt3)/(2)`
Solve for x : sin2 x + sin2 30° = 1
Solve for x : cos2 30° + cos2 x = 1
Solve for x : cos2 30° + sin2 2x = 1
Solve for x : sin2 60° + cos2 (3x- 9°) = 1
If 4 cos2 x = 3 and x is an acute angle;
find the value of :
(i) x
(ii) cos2 x + cot2 x
(iii) cos 3x (iv) sin 2x
In ΔABC, ∠B = 90° , AB = y units, BC = `(sqrt3)` units, AC = 2 units and angle A = x°, find:
- sin x°
- x°
- tan x°
- use cos x° to find the value of y.
If 2 cos (A + B) = 2 sin (A - B) = 1;
find the values of A and B.
Solutions for 23: Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios]
![Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 23 - Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios] Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 23 - Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios] - Shaalaa.com](/images/concise-mathematics-english-class-9-icse_6:b313c06da7fb4b0f885a06c3b5e4e4fa.jpg)
Selina solutions for Concise Mathematics [English] Class 9 ICSE chapter 23 - Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios]
Shaalaa.com has the CISCE Mathematics Concise Mathematics [English] Class 9 ICSE CISCE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Selina solutions for Mathematics Concise Mathematics [English] Class 9 ICSE CISCE 23 (Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios]) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Selina textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Concise Mathematics [English] Class 9 ICSE chapter 23 Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios] are Trigonometric Equation Problem and Solution, Trigonometric Ratios of Some Special Angles, Trigonometric Ratios of Some Special Angles, Trigonometric Ratios of Some Special Angles.
Using Selina Concise Mathematics [English] Class 9 ICSE solutions Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios] exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Selina Solutions are essential questions that can be asked in the final exam. Maximum CISCE Concise Mathematics [English] Class 9 ICSE students prefer Selina Textbook Solutions to score more in exams.
Get the free view of Chapter 23, Trigonometrical Ratios of Standard Angles [Including Evaluation of an Expression Involving Trigonometric Ratios] Concise Mathematics [English] Class 9 ICSE additional questions for Mathematics Concise Mathematics [English] Class 9 ICSE CISCE, and you can use Shaalaa.com to keep it handy for your exam preparation.
